Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 10.Problemas - Ex. 111
O ciclo de turbina a gás de uma usina de ciclo combinado gás-vapor tem uma razão de pressão igual a 12. O ar entra no compressor a 310 K, e na turbina, a 1400 K. Os gases de combustão que saem da turbina a gás são utilizado para aquecer o vapor a 12,5 MPa até 500 °C em um trocador de calor. Os gases de combustão saem do trocador de calor a 247 °C. O vapor se expande em uma turbina de alta pressão até 2,5 MPa e é reaquecido na câmara de combustão até 550 °C antes de se expandir em uma turbina de baixa pressão até 10 kPa. O fluxo de massa do vapor é de 12 kg/s. Considerando que todos os processos de compressão e expansão sejam isentrópicos, determine (a) o fluxo de massa do ar no ciclo de turbina a gás, (b) a taxa total de fornecimento de calor e (c) a eficiência térmica de ciclo combinado.
Passo 1
Tá legal, vamos primeiro ilustrar o diagrama T-s do ciclo gás-vapor com reaquecimento na câmara de combustão, então, teremos:
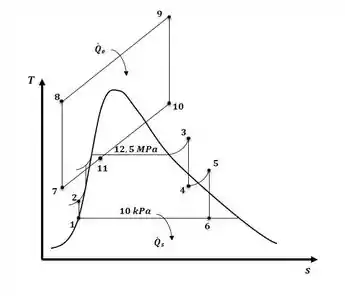
Agora, o que nós vamos fazer é trabalhar com o ciclo a gás para descobrir o valor das propriedades nos pontos de interesse. Então, com a ajuda das tabelas termodinâmicas do apêndice A, vamos determinar as propriedades dos pontos 7 a 11. Então, começando pelo ponto 7, temos:
Então, com a pressão relativa em 7, podemos obter a pressão relativa em 8 através de:
E, com esse valor de pressão relativa, recorrendo às tabelas do apêndice A, temos a seguinte entalpia para o ponto 8:
Continuando, agora analisando o ponto 9, temos:
Então, da mesma forma que fizemos acima, podemos encontrar o valor da pressão relativa no ponto 10:
E, com esse valor de pressão relativa, recorrendo às tabelas do apêndice A, temos a seguinte entalpia para o ponto 10:
Continuando, agora analisando o ponto 11, temos:
Passo 2
Agora nós vamos encontrar as propriedades do ciclo a vapor com a ajuda das temperaturas e pressões e consultando as tabelas do apêndice A, então, temos:
Com isso, podemos encontrar o trabalho consumido pela bomba 1 através de:
E, com esse valor, aplicando o equilíbrio de energia para a bomba 1, podemos encontrar o valor da entalpia no ponto 2:
Agora, continuando com as propriedades, temos:
Então, podemos encontrar o título nessa condição:
E, com esse valor, encontrar a entalpia nesse ponto:
Passo 3
Agora nós vamos aplicar o equilíbrio de energia para o trocador de calor, dessa forma, teremos:
Como no nosso caso temos regime permanente, então , dessa forma, a equação se torna:
E, colocando em função das entalpias e das vazões mássicas, temos:
Então, substituindo os valores conhecidos, temos:
Passo 4
Agora, para a letra (b), nós vamos calcular o calor total que foi adicionado ao sistema, que entra pela câmara de combustão e devido ao reaquecimento, então, temos:
Então, substituindo os valores conhecidos, temos:
Passo 5
Agora, o calor que sai do sistema pode ser encontrado pela soma do calor que deixa o sistema no trocador de calor e no condensador, então, temos:
Substituindo os valores conhecidos, temos:
E, então, a eficiência térmica do ciclo será: