Enunciado
Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 5.Problemas - Ex. 73
Um cilindro com um pistão restringido por uma mola linear, contém de bióxido de carbono a e . O conjunto é então resfriado até , ponto no qual a pressão é de . Calcule a transferência de calor no processo.
Passo 1
Fala, galera! Nessa questão nós temos um cilindro com uma massa de , sendo resfriado, e nós temos que calcular a transferência de calor nesse processo. Para isso, vamos usar a primeira lei da termodinâmica na forma:
Nós vamos olhar na Tabela A.8 para achar as energias internas inicial e final, usando as temperaturas que o enunciado nos deu, e vamos calcular o trabalho pela definição:
Que é numericamente igual a área sob o diagrama que nós vamos construir.
Passo 2
Vamos começar determinando os volumes para construir nosso diagrama . Considerando o como um gás ideal, temos a equação:
Isolando o volume , temos:
Na Tabela A.5 achamos . O enunciado deu as temperaturas:
Então no estado inicial o volume é:
E no estado 2,
Passo 3
Com os volumes determinados podemos desenhar o nosso diagrama para calcular o trabalho.
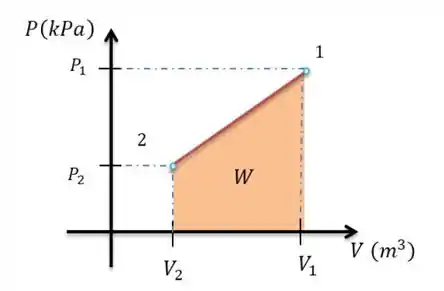
O trabalho é a área sob o diagrama:
Aqui nós temos uma área de trapézio, que pode ser calculada por:
Passo 4
Agora podemos calcular o calor transferido no processo. Mas para finalizar, temos que encontrar a energia interna em cada estado.
Olhando na Tabela A.8, para a temperatura , nosso valor está entre e , fazendo uma média simples:
Para o estado final, com , nosso valor está mais próximo de , então vamos fazer uma aproximação:
Substituindo todos os resultados na fórmula do calor, temos:
É isso, galera, encerramos o exercício 😉.