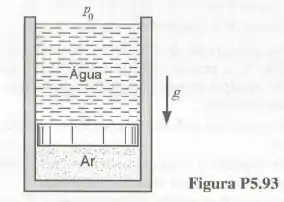
A Fig. P5.93 mostra um conjunto cilindro-pistão com área de seção transversal igual a e altura de . O pistão, que é muito fino e tem massa desprezível, separa a câmara em duas regiões. Inicialmente, a região superior contém água a e a inferior contém de ar a . Transfere-se então, calor à região inferior de modo que o pistão inicia o movimento e provocando, assim, o transbordamento na região superior. Este processo continua até que o pistão superior. Este processo continua até que o pistão alcança o topo do cilindro. Admitindo os valores normais para e , determine o calor transferido para o ar no processo.

Vamos começar com o cálculo da pressão inicial.

A pressão inicial configura a pressão atmosférica mais a pressão da coluna de água, escrevendo isso matematicamente, temos:

Para finalizarmos o cálculo da pressão inicial temos que determinar a massa da água:

Olhando na tabela a água sobe condições de e , temos:

Substituindo a massa no cálculo da pressão inicial, temos:

Vamos analisar as condições no estado final.

No final do processo temos que a água toda foi despejada e temos uma pressão atuando sobe o pistão a atmosférica, portanto:

E volume o final, temos o volume todo só ar:

Para o cálculo da temperatura final, a temperatura esta diretamente ligada com a variação da pressão e volume, portanto, existe uma relação de proporção que a seguinte:

Isolando e substituindo dados, temos:

Com todas as condições de estado definidas vamos calcular o trabalho.

A fórmula do trabalho se da pela área integrável do diagrama , então bora desenhar o diagrama pra entendermos melhor qual área teremos que calcular:

O trabalho será igual à área sobe a nossa reta:

Temos a área de um trapézio, a área de um trapézio se calcula pela soma das bases dividida por 2 multiplicado pela altura.

Finalmente poderemos partir para o cálculo do calor transferido no processo.

Utilizando a fórmula enunciada no passo 1:

Olhando na tabela , temos

Substituindo valores:

Fecho galera é isso ae.