Enunciado
Termodinâmica - Termodinamica,Teoria Cinética e Termodinâmica Estatística, Sears e Salinger- Ed: 3º - Capítulo 2.Problemas - Ex. 11
Um cilindro provido de um êmbolo móvel contém uma certa quantidade de ar. Inicialmente, a pressão do ar é , o volume é e a temperatura é . Suponha que o ar seja um gás ideal. (a) Qual é o volume final do ar se ele se expande isotermicamente até uma pressão de , sendo que o êmbolo se move para fora para permitir o aumento de volume do ar? (b) Qual sera a temperatura final do ar se o êmbolo permanecer fixo em sua posição inicial e o sistema for resfriado até que a pressão seja de ? (c) Quais são a temperatura e o volume finais do ar, se ele se expande isotermicamente das condições iniciais até a pressão de e, então, ele é resfriado a volume cons- tante até que a pressao seja de ? (d) Quais são a temperatura e o volume finais do ar, se um resfriamento isocórico até e seguido por uma expansão isotérmica até ? (e) Faça um gráfico destes processos em um diagrama .
Passo 1
Fala, galerinha. Estamos aqui pra mais um exercício, mas calma que vou te ajudar nessa.
Nesse exercício temos alguns processos do ar em uma seringa e ele quer algumas informações sobre isso. Vamos ver como fica cada uma dessas situações.
Passo 2
Primeiro ele quer o volume em uma expansão isotérmica. Assim vamos ter a equação geral dos gases
Como é uma expansão isotérmica, temos que . Assim, a equação fica
Como ele quer o volume final, ele quer o . Então isolando ele, temos
Substituindo os valores, temos
Passo 3
Agora queremos a temperatura final se o volume ficar constante. Novamente vemos a equação geral dos gases. Como o volume é constante, vamos ter . Então a equação fica
Isolando temos
Passo 4
Nessa questão temos dois processos, então vamos dividir pra não fazer confusão.
O primeiro processo é uma expansão isotérmica das condições iniciais até uma pressão de . Então vamos calcular qual é o volume atingido nesse primeiro processo. Pela equação geral e considerando que isotérmico quer dizer que a temperatura é constante, temos
Isolando temos
O segundo processo é resfriar a volume constante. Uma informação importante que agora a pressão é e não mais , que vai ser a pressão final . A equação então vai ficar
Isolando temos
Passo 5
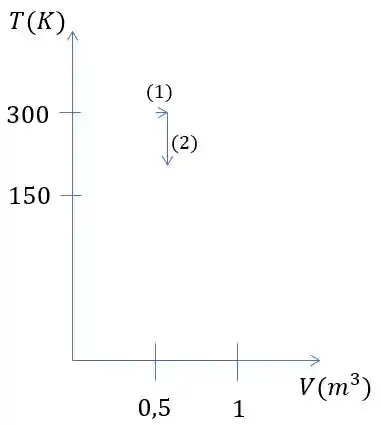
Agora o gráfico dessas transformações em um diagrama .
O gráfico das letras e estão representadas na imagem a seguir
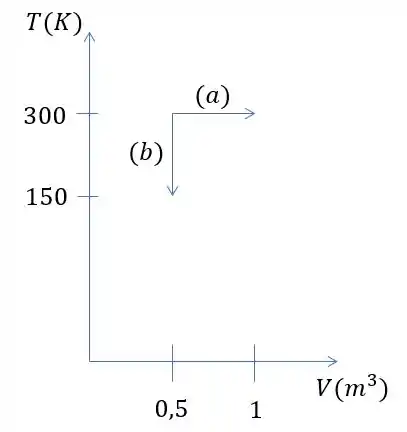
Para a letra já temos
Mais um problema feito. Bora pra mais um?
Resposta
