Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 8.Problemas - Ex. 126

Um cilindro rígido com 50   L nitrogênio está equipado com uma válvula de segurança ajustada em 1.200   k P a . Inicialmente, esse cilindro contém nitrogênio a 1.200   k P a e 20   ° C . Calor e então transferido para o nitrogênio de um reservatório de energia térmica a 500   ° C , e uma quantidade de nitrogênio escapa até que sua massa se torna a metade do valor inicial. Determine a mudança no potencial de trabalho do nitrogênio, resultado desse aquecimento.

Considere T 0 = 20   ° C .

Passo 1

Vamos lá! A questão nos afirma que um tanque rígido contendo nitrogênio é considerado. O calor é agora transferido para o nitrogênio de um reservatório e o nitrogênio é permitida a fuga até que a massa de nitrogênio se torne metade da sua massa inicial. A mudança no trabalho do nitrogênio. O potencial deve ser determinado.

Podemos simplificar o problema como:

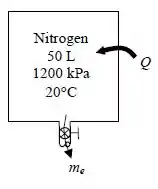
Assumindo que:

  1. Este é um processo instável, uma vez que as condições dentro do dispositivo estão mudando durante o processo.
  2. As energias cinéticas e potenciais são insignificantes.
  3. Não há interações de trabalho envolvidas.
  4. O nitrogênio é um gás ideal com constantes e específicas.

As propriedades do nitrogênio à temperatura ambiente são c p   =   1 . 039   k J / k g ⋅ K , c v =   0 . 743   k J / k g ⋅ K , e R   =   0 . 2968   k J / k g ⋅ K (Tabela A-2a).

Passo 2

Pronto já temos todas as informações necessárias, vamos para a análise. As massas inicial e final no tanque são

m 1 = P V R T 1 = 1200   k P a 0.050   m 3 0.2968   k P a ∙ m 3 k g ∙ K 293   K = 0.690   k g

m 2 = m e = m 1 2 = 0.690   k g 2 = 0.345   k g

A temperatura final no tanque é de

T 2 = P V m 2 R =   1200   k P a 0.050   m 3 0.2968   k P a ∙ m 3 k g ∙ K 0.345   k g = 586   K .

Passo 3

Nós tomamos o tanque como o sistema, que é um volume de controle desde que a massa atravessa o limite. Observando que as energias microscópicas de fluidos e não fluidos são representadas pela entalpia h e energia interna u , respectivamente, os balanços de massa e energia para este sistema de fluxo uniforme podem ser expressos como

Equilíbrio de massa:

m i n - m o u t = Δ m s y s t e m → m e = m 2

Balanço energético:

E i n - E o u t = Δ E s y s t e m

Q i n - m e h e = m 2 u 2 - m 1 u 1

Q o u t = m e h e + m 2 u 2 - m 1 u 1

Usando a média das temperaturas inicial e final para o nitrogênio à saída, T e   =   0,5 ( T 1   +   T 2   )   =   0,5 ( ( 293   +   586 )   =   439,5   K   esta equação de balanço energético torna-se

Q o u t = m e h e + m 2 u 2 - m 1 u 1

= m e c p T e + m 2 c v T 2 - m 1 c v T 1

= 0.345 1.039 439.5 + 0.345 0.743 586 - 0.690 0.743 293

= 157.5   k J

Passo 4

Certo! Agora vamos analisar o potencial de trabalho associado a este processo é igual ao esforço destruído durante o processo. A destruição de energia durante um processo pode ser determinada a partir de um equilíbrio de energia ou diretamente a partir da sua definição X d e s t r u i d a = T 0 S g e r a d a . A entropia geração S g e r a d a neste caso é determinada a partir de um balanço de entropia no sistema:

S i n - S o u t + S g e n = Δ S s y t e m

Q i n T R - m e s e + S g e n = Δ S t a n q u e = m 2 s 2 - m 1 s 1

S g e n = m 2 s 2 - m 1 s 1 + m e s e - Q i n T R

= m s c p ln ⁡ T 2 - m 1 c p ln ⁡ T 1 + m e c p ln ⁡ T e - Q i n T R

= 0.345 1.039 ln ⁡ 586 - 0.690 1.039 ln ⁡ 293 + 0.345 1.039 ln ⁡ 439.5 - 157.5 773

= 0.190   k J / K

Então,

W r e v = X d e s t r u í d o = T 0 S g e n = 293   K 0.190 k J K =   55.7   k J

Resposta

55.7   k J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o trabalho necessário para dobrar reversível e isotermicamente a magnetização em um bastão paramagnético cilíndrico e fino, que preenche o volume V de um solenoide cilíndrico coaxial de N espi
Calcule o trabalho necessário para remover fino bastão paramagnético de um solenoide coaxial perfeitamente ajustado a ele. O solenoide tem resistência nula e a intensidade magnética constante. Suponha
Faça um esboço das variações da energia interna, quando o volume do sistema do problema anterior varia durante os processos mostrados na figura 3.17
Considere um sistema consistindo de um cilindro contendo 0,2 quilomol de um gás ideal e equipado com um pistão sem massa de 0,5m 2 de área. A força de atrito entre o pistão e as paredes do cilindro e
considere somente os processos adiabáticos que transformam um sistema do estado a Para o estado d , como é mostrado na figura acima. As duas curvas , a - c - e e b - d - f , são processos adiabáticos