Enunciado
Termodinâmica - Termodinamica,Teoria Cinética e Termodinâmica Estatística, Sears e Salinger- Ed: 3º - Capítulo 3.Problemas - Ex. 20
considere somente os processos adiabáticos que transformam um sistema do estado
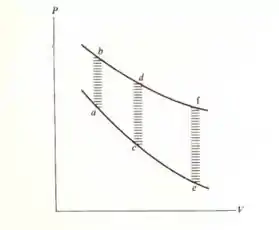
Para o estado , como é mostrado na figura acima. As duas curvas são processos adiabáticos reversíveis. Os processos indicados por hachuras não são reversíveis.
a) prove que o trabalho total realizado ao longo das trajetórias é mesmo.
b) mostre que o trabalho de configuração ao longo de é nulo.
c) mostre que o trabalho dissipativo ao longo da trajetória é maior que ao longo da trajetória , e menor que ao longo da trajetória
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão do livro de termodinâmica de Sears e Salinger considerando somente os processos adiabáticos que transformam um sistema do estado
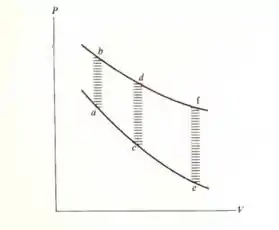
Para o estado , como é mostrado na figura acima. As duas curvas são processos adiabáticos reversíveis. Os processos indicados por hachuras não são reversíveis.
a) prove que o trabalho total realizado ao longo das trajetórias é mesmo.
b) mostre que o trabalho de configuração ao longo de é nulo.
c) mostre que o trabalho dissipativo ao longo da trajetória é maior que ao longo da trajetória , e menor que ao longo da trajetória
Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Então galerinha nessa questão ele dá a imagem em que demonstra o processo adiabático em que são processos adiabáticos reversíveis, temos
Na letra (a) para provar o trabalho realizado na trajetória que,
Já para,
E no trabalho,
Já na letra (b) para mostrar o trabalho de configuração em que ao longo de , temos
Logo fazendo as separações vamos ter que,
Logo,
E por fim na letra para mostrar o trabalho dissipativo ao longo da trajetória fica,
Ficando,
Ficando a definição de trabalho no trajeto por,
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.
Resposta
a) , e
b)
c)