Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 4.Problemas - Ex. 17

Um conjunto cilindro-pistão contém 3   k g de ar a 20   ° C e 300   k P a . O conjunto é então aquecido em um processo a pressão constante até 600   K .

a. Determine o volume final

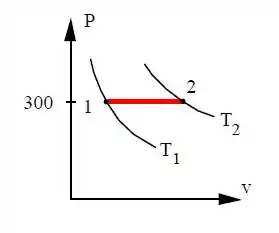
b. Trace um gráfico da linha do processo em um diagrama p - v

c. Determine o trabalho no processo.

Passo 1

Vamos lá, pessoal! Vamos assumir que o ar é um gás ideal e usar a Lei dos gases:

P V = m R T

A partir dessa equação podemos usar os dados do enunciado para calcular o volume no estado 1.

P 1 V 1 = m R T 1

Isolando V 1 ,

V 1 = m R T 1 P 1 = ( 3   k g ) ( 0,287   k J / k g ∙ K ) ( 20 + 273,15 K ) 300   k P a

V 1 = 0,8413   m 3

No estado 2, nós temos T 2 = 600   K e P 2 = P 1 , então podemos calcular o volume 2 da mesma forma:

V 2 = m R T 2 P 2 = ( 3   k g ) ( 0,287   k J / k g ∙ K ) ( 600 K ) 300   k P a

V 2 = 1,722   m 3

Encontramos o volume final.

Passo 2

Determinando o trabalho no processo, a pressão constante nós podemos calcular:

W = ∫ P d V = P ( V 2 - V 1 )

W = 300   k P a 1,722 - 0 , 8413 m 3

W = 264,2   k J

Passo 3

Montando o diagrama P - V do processo, temos:

Resposta

1,722   m 3

D i a g r a m a   P - V

264,2   k J

Exercícios de Livros Relacionados

Uma determinada massa de ar com n = 1,5 inicialmente a 2 Mpa e 300 °C é expandida em um processo politrópico para 80 kPa em um arranjo pistão-cilindro. Determine a temperatura final do ar.
Obtenha uma expressão geral para o trabalho produzido por um gás ideal quando ele passa por um processo politrópico em um sistema fechado do estado inicial 1 ao estado final 2. Para o resultado, deve-
Uma massa de 5 kg de uma mistura de água líquida e vapor de água saturados está contida em um arranjo pistão-cilindro a 125 kPa. Inicialmente, dois quilos de água estão na fase líquida e o restante na
Um arranjo pistão-cilindro sem atrito contém inicialmente ar a 100 kPa e 0,15 m³. Nesse estado, uma mola linear ( F ∝ x ) está tocando o pista, mas sem exercer qualquer força sobre o mesmo. O ar é ent
Hélio inicialmente a 1.500k P a e 300° C e expandido em uma turbina ate 100k P a e25° C . Determine o trabalho máximo que essa turbina pode produzir, em k J / k g . O trabalho maximo exige uma turbina