Enunciado
Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 8.Problemas - Ex. 94
Um conjunto cilindro-pistão contém ar na condição ambiente, e , com um volume de . O ar é comprimido até em um processo politrópico reversível com expoente , após o que é expandido de volta a em um processo adiabático reversível.
a. Mostre os dois processos em diagramas e .
b. Determine a temperatura final e o trabalho líquido.
Passo 1
Fala, galera! Nessa questão nós temos uma compressão politrópica reversível, seguida de um processo de expansão adiabática reversível. Colocando isso nos diagramas e , temos:
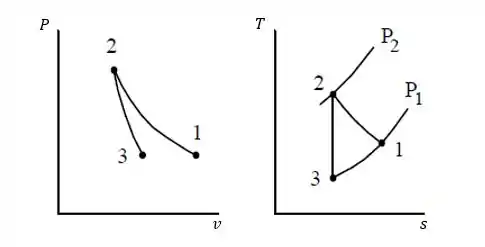
Essa é a nossa letra a.
Passo 2
Na letra b, nós precisamos determinar a temperatura final e o trabalho líquido nos dois processos.
Primeiro, na compressão politrópica reversível, vamos encontrar a temperatura final usando a equação:
O enunciado nos dá:
Substituindo tudo na relação da temperatura:
O trabalho é dado pela equação:
Na Tabela A.5, temos . Substituindo os valores:
Passo 3
Para o processo adiabático reversível, o enunciado nos dá:
E então, vamos usar a relação:
Substituindo dos valores:
E o trabalho é dado pela equação:
Na Tabela, temos . Substituindo os valores:
Passo 4
Para calcular o trabalho líquido de todo o processo, vamos precisar da massa. Admitindo um gás ideal nesse caso, vamos usar a equação dos gases:
Substituindo os valores:
Calculando o trabalho líquido:
É isso, galera, valeu! 😉.
Resposta
e