Considere um motor térmico de Carnot que utiliza água como fluido de trabalho A transferência de calor para a água ocorre a e neste processo a água se transforma de líquido saturado para vapor saturado. Sabendo que o reservatório a baixa temperatura está a ,
a) Mostre o ciclo num diagrama ;
b) Determine o título da água no início e no término da transferência de calor para a fonte fria;
c) Determine o trabalho líquido, por quilograma de água, e o rendimento térmico deste ciclo.
Passo 1
E ai galera! Vamos iniciar a resolução de mais uma questão de termodinâmica, vem comigo!
Letra a)
Começamos o problema representando o ciclo de Carnot num diagrama :
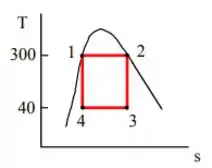
Bora pra letra b!
Passo 2
Letra b)
Para determinarmos o título da água no início da transferência de calor temos que primeiramente buscarmos na Tabela B.1.1 o valor da entropia de vapor saturado e líquido saturado para a água saturada a :
Como a estropia nos pontos 2 e 3 são iguais, assim como nos pontos 1 e 4, temos:
Na mesma tabela, precisamos obter os valores de entropia de liquido saturado e de evaporação para a água saturada sob a temperatura de :
Passo 3
Agora, calculamos a título da água no ponto 3, onde se inicia a transferência de calor:
Substituindo os dados:
Seguindo, calcularemos o título da água no final da transferência de calor que se dá no ponto 4:
Bem simples né?
Passo 4
Letra c)
Aqui, calcularemos primeiro o rendimento do ciclo, que é dado pela equação:
Dados:
;
.
Temos:
Passo 5
A partir da equação:
Conseguimos calcular o calor transferido no ciclo:
Assim, voltando na primeira equação apresentada para o cálculo de rendimento, obtemos o trabalho líquido:
Diz pra mim, foi mais simples do que pensava né?
Até a próxima questão!
Resposta
a) Gráfico
b) ,
c) ,