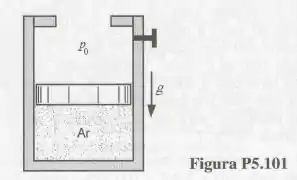
O conjunto cilindro-pistão mostrado na Fig. contém, inicialmente, ar a e (estado 1). O ar é expandido, num processo a pressão constante até que o volume se torne igual ao dobro do inicial (estado 2). Neste ponto, o pistão é travado com um pino e transfere-se calor do ar até que a temperatura atinja (estado 3). Determine , e para os estados e e calcule os trabalhos realizados e a transferências de calor no dois processos

Vamos começar determinar e do estado 2.

Bem a pressão ele nos deu.

Para encontrar a temperatura vamos considerar o ar como um gás ideal. Com está condição temos que a relação da temperatura e volume é linear.

Como o volume no estado 2 é o dobro do inicial, temos:

Para determinar a entalpia, temos que consideramos o ar um gás ideal, logo, podemos olhar na tabela para , fica:

Já que estamos olhando na tabela vamos aproveitar e determinar pra o estado 1. Para fica:

Para será igual por causa de, .

Para encontrar a pressão no estado 3, temos que utilizar a mesma relação de linearidade.

Temos que a relação da pressão e temperatura são lineares devido, ao gás ideal e o conjunto.

Falta determinar o trabalho e o calor transferido de cada processo.

Determinando o trabalho do estado 1 ao 2.

Trabalho com a pressão constante pode ser calculado da seguinte forma:

Calculando o volume inicial pela fórmula do gás ideal, fica:

Utilizando o volume como volume específico e olhando na tabela o , fica:

Substituindo no trabalho:

Para o trabalho do estado 2 ao 3 temos que ele configura como zero. Pois, o volume é constante.

Calculando o calor transferido para cada processo.

Utilizando a equação da energia que é a seguinte:

Substituindo o trabalho na equação:

Do processo 1 ao 2, fica:

Do processo 2 ao 3:

Como do ao nós não temos trabalho, teremos que utilizar a energia interna do sistema.

Para isto teremos que olhar na tabela para o é , para temos

Aplicando a fórmula, temos:

Ufa acabamos, essa foi grande. Valeu galera até a próxima.