Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 3.Problemas - Ex. 51

Um conjunto cilindro-pistão tem 1,5   k g de ar a 300   K e 150   k P a . O arranjo é então aquecido em um processo de duas etapas, primeiramente a volume constante até 1000   K (estado 2), e em seguida, a pressão constante até 1500   K (estado 3).

a. Determine o volume nos estados 2 e 3.

b. Determine a pressão final.

c. Esboce um diagrama p - v mostrando os processos ocorridos.

Passo 1

Vamos lá, pessoal! Nós temos dois processos:

1 - 2 : p r o c e s s o   a   v o l u m e   c o n s t a n t e → V 2 = V 1

2 - 3 : p r o c e s s o   a   p r e s s ã o   c o n s t a n t e → P 3 = P 2

Para determinar o volume no estado 2 ( V 2 ) vamos considerar a Lei dos gases, assumindo que esse seja um gás ideal:

P 1 V 1 = m R T 1

Da Tabela A.5 temos que R = 0,287   k J / k g ∙ K . Assim, substituindo os valores na equação e isolando V 1 , temos:

V 1 = m R T 1 P 1 = 1,5 × 0,287 × 300 150

V 1 = 0,861   m 3 = V 2

Determinamos o volume no estado 2, como pediu o item a, falta o volume no estado 3.

Passo 2

Vamos lá! Usando a relação de proporção do sistema:

V 3 V 2 = T 3 T 2

Isolando V 3 e substituindo os resultados, temos:

V 3 = V 2 T 3 T 2 = 0,861 × 1500 1000 = 1,2915   m 3

Encontramos o volume no estado 3.

Passo 3

Para calcular a pressão final, conforme pede o item 2, vamos usar a relação:

P 2 P 1 = T 2 T 1

Isolando P 2 e substituindo os valores:

P 2 = P 1 T 2 T 1 = 150 × 1000 300

P 2 = 500   k P a  

Encontramos a pressão final.

Passo 4

Esboçando o diagrama p - v para os processos:

1 - 2 : p r o c e s s o   a   v o l u m e   c o n s t a n t e → V 2 = V 1

2 - 3 : p r o c e s s o   a   p r e s s ã o   c o n s t a n t e → P 3 = P 2

Temos:

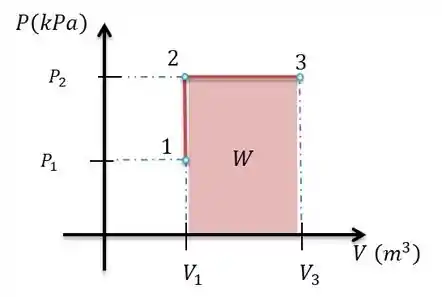
Onde W é o trabalho realizado pelo sistema.

Resposta

a. V 2 = 0,861   m 3 , V 3 = 1,2915   m 3 ,

b. P 2 = 500   k P a ,

c. Diagrama p - v .

Exercícios de Livros Relacionados

O ar num tanque está a 1M P a e a temperatura ambiente de 20° C . O ar é utilizado para encher um balão inicialmente vazio até uma pressão de 200k P a , na qual o diâmetro do balão é de 4m e a tempera
Vapor saturado de R-134ª a 50°C varia seu volume a temperatura constante. Determine os novos valores de pressão e de título (se saturado) se o volume dobrar. Repita a questão para o caso em que o volu
Vapor d’água saturado a 200 kPa está no interior de um conjunto cilindro-pistão de pressão constante. Neste estado, o pistão está a 0,1m do fundo do cilindro. Qual será essa distância e a temperatura
Vapor d’água saturado a 60°C deve ter sua pressão diminuída para que o volume aumente em torno de 10% enquanto a temperatura permanece constante. A que pressão deve o vapor ser expandido?
Uma jarra de vidro é enchida com vapor saturado a 500k P a e 25 % de título e tampada firmemente. Em seguida, o conjunto é resfriado até - 10 ° C . Qual é a fração em massa de sólido nessa temperatura