Enunciado
Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 8.Problemas - Ex. 14
Considere uma bomba em um ciclo de calor com o como fluido de trabalho. Calor é rejeitado do a durante um processo no qual o a muda de vapor saturado para líquido saturado. O calor é transferido para o a .
- Mostre o ciclo em um diagrama
- Determine o título do no início e no final do processo isotérmico de transferência de calor a
- Determine o coeficiente de performance do ciclo
Passo 1
Fala pessoal, tudo tranks?
No nosso problema, temos uma bomba em um ciclo de calor com o como fluido de trabalho. Calor é rejeitado do a durante um processo no qual o a durante um processo no qual o muda de vapor saturado para líquido saturado. O calor é transferido para o a .
E como pede o exercício, vamos começar então fazendo o esboço do nosso ciclo em um diagrama T-s
a) Temos então, que...
Passo 2
b) Feito o esboço do nosso ciclo, vamos então atrás das entropias. Porque nessa letra aqui, temos que achar o título do no início e no final do processo isotérmico de transferência de calor a
De acordo com a tabela abaixo...
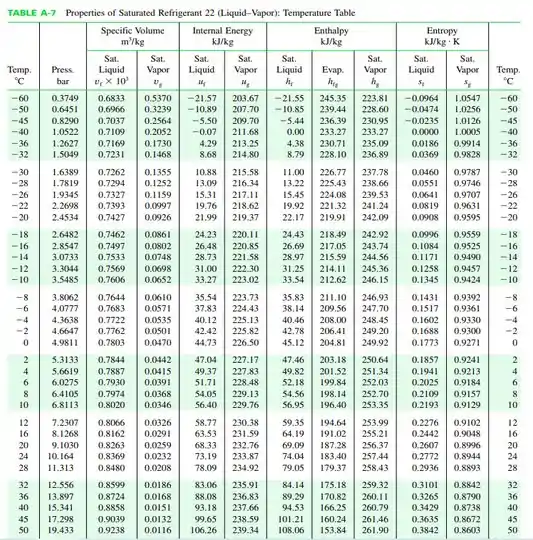
Dando uma olhada nessa figura e com base no ciclo que a gente esboçou no Passo 1, temos que...
Onde...
Sendo assim, usando a fórmula abaixo...
Podemos obter os títulos correspondentes...
Passo 3
c) Por último, falta determinar o coeficiente de performance do ciclo
Sabemos que ele é dado pela seguinte fórmula...
Mas essa fórmula também pode ser escrita como...
Sendo assim, basta substituir com as temperaturas quente e frio do enunciado em :
Pronto! Finalizamos aqui!
Resposta
a)
b)
c)