Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 7.Problemas - Ex. 57

Vapor saturado entra em um bocal adiabático que opera em regime permanente com baixa velocidade de entrada a 6 Mpa, expandindo-se até 1,2 MPa.

(a) Considerando uma situação em que a velocidade de saída tenha o máximo valor possível, esboce um diagrama T-s com relação às linhas de saturação para esse processo.

(b) Determine a máxima velocidade de saída do vapor, em m/s.

Passo 1

Entendendo o problema (item A):

O processo consiste em um vapor saindo que percorre um bocal, em regime permanente de escoamento, expandindo-se de uma maneira adiabática (sem transferência de calor). O problema pede o diagrama temperatura X entropia do processo e a máxima velocidade na saída do bocal. O diagrama é mostrado na figura 1:

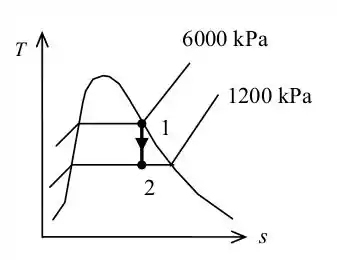
Figura 1: Diagrama T x s, para o processo adiabático

Como observado, inicialmente o sistema encontra-se sob forma de vapor saturado e após a expansão a saída do bocal é uma mistura líquido-vapor.

Passo 2

Coletando dados (item B):

Na entrada do bocal:

(vapor saturado)

Consultando a tabela A-5 do livro:

Na saída do bocal:

Uma vez que o problema pede a velocidade máxima na saída do bocal, essa condição é atendida quando a entropia do sistema se conserva da entrada para a saída. Assim: