Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 94
Considere um ciclo Brayton simples que utiliza ar como fluido de trabalho, tem uma razão de pressão igual a , uma temperatura máxima de ciclo de e opera na admissão do compressor a . O que terá o maior impacto na razão de consumo de trabalho: uma eficiência isentrópica do compressor correspondente a ou uma eficiência isentrópica da turbina igual a ? Considere calores específicos constantes à temperatura ambiente.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Em questões de ciclos termodinâmicos é sempre bom desenhar o ciclo que se está utilizando para ajudar a identificar cada estado e processo envolvido.
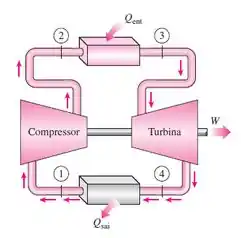
Nessa questão por exemplo, trata-se do ciclo Brayton simples não ideal. Seu diagrama é dado por:
Primeiro vamos anotar os dados da questão:
Como devemos considerar calores específicos constantes a temperatura ambiente, podemos usar as relações envolvendo para descobrir os dados que não sabemos.
Passo 2
Agora vamos analisar os processos. O processo é uma compressão isentrópica, logo:
Sabendo que:
Temos que:
Substituindo os valores temos que:
Passo 3
Como devemos considerar o compressor não é ideal quando a turbina for ideal, temos que aplicar a sua eficiência isentrópica para descobrir a verdadeira temperatura na saída do compressor. (Estado ).
Substituindo os valores, temos que:
Passo 4
O processo é uma expansão isentrópica, logo:
Sabendo que:
Temos que:
Substituindo os valores temos que:
Passo 5
O exercício nos pede para considerar a turbina não ideal quando o compressor for ideal, por isso devemos aplicar a eficiência isentrópica da turbina para encontrar o valor real da entalpia no estado :
Substituindo os valores, temos que:
Resolvendo, temos que:
Passo 6
Agora que sabemos as temperaturas de cada estado, podemos calcular os trabalhos de turbina e compressor quando forem isentrópicos ou não.
Para o compressor isentrópico, temos que:
Para o compressor real, temos que:
Passo 7
Para a turbina isentrópica, temos que:
Para a turbina real, temos que:
Passo 8
Agora vamos calcular as razões de consumo de trabalho para cada situação descrita no enunciado e avaliar qual terá o maior impacto na razão de consumo de trabalho.
A primeira situação é de que a eficiência isentrópica no compressor corresponda a . Ou seja, o compressor será real e a turbina ideal:
Substituindo os valores, temos que:
Para a segunda situação, devemos considerar um sistema onde a eficiência isentrópica da turbina seja de . Ou seja, neste caso a turbina será real e o compressor ideal:
Substituindo os valores, temos que:
Ou seja, o impacto é praticamente o mesmo para os casos de sistemas com turbinas com eficiências isentrópicas de ou de sistemas com compressores com eficiências isentrópicas de .
Resposta
O impacto é praticamente o mesmo para os casos de sistemas com turbinas com eficiências isentrópicas de ou de sistemas com compressores com eficiências isentrópicas de .