Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 89
Um ciclo Brayton simples que usa ar como fluido de trabalho tem uma razão de pressão igual a . As temperaturas mínima e máxima do ciclo são e respectivamente. Considerando uma eficiência isentrópica de para o compressor e de para a turbina, determine (a) a temperatura do ar na saída da turbina, (b) o trabalho líquido produzido e (c) a eficiência térmica.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Em questões de ciclos termodinâmicos é sempre bom desenhar o ciclo que se está utilizando para ajudar a identificar cada estado e processo envolvido.
Nessa questão por exemplo, trata-se do ciclo Brayton simples não ideal. Seu diagrama é dado por:
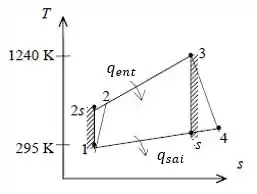
Primeiro vamos anotar os dados da questão:
Como devemos considerar calores específicos variáveis com a temperatura, temos que usar a tabela para obter os valores de entalpia e pressão relativa para cada temperatura.
Para , temos que:
Para , temos que:
Passo 2
Agora vamos analisar os processos. O processo é uma compressão isentrópica, logo:
Sabendo que:
Temos que:
Substituindo os valores temos que:
Analisando novamente a Tabela, podemos interpolar os valores para encontrar a entalpia no estado :
Passo 3
Porém... o nosso processo não é ideal, por isso devemos aplicar a eficiência isentrópica do compressor para encontrar o valor real da entalpia no estado :
Substituindo os valores, temos que:
Resolvendo, temos que:
Passo 4
O processo é uma expansão isentrópica, logo:
Sabendo que:
Temos que:
Substituindo os valores temos que:
Analisando novamente a Tabela, podemos interpolar os valores para encontrar a entalpia no estado :
Passo 5
Porém... a turbina, assim como compressor não é ideal, por isso devemos aplicar a eficiência isentrópica da turbina para encontrar o valor real da entalpia no estado :
Substituindo os valores, temos que:
Resolvendo, temos que:
A temperatura real no estado , analisando a tabela e interpolando será:
Passo 6
Agora que sabemos as entalpias de cada estado, podemos calcular o trabalho exigido pelo compressor e o trabalho realizado pela turbina.
Substituindo os valores, temos que:
Para o compressor:
Para a turbina:
Passo 7
A eficiência térmica é dada por:
O calor fornecido é dado por:
Logo:
O trabalho líquido pode ser descrito como o trabalho fornecido menos o trabalho requerido .
Portanto, a eficiência térmica será:
Ou: