Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 6.Problemas - Ex. 132
Considere um ciclo de refrigeração de Carnot executado em um sistema fechado, na região de mistura líquido-vapor saturada, utilizando 0,96 kg de refrigerante-134a como fluido de trabalho. Sabe-se que a temperatura absoluta máxima do ciclo e igual a 1,2 vez a temperatura absoluta mínima e que o trabalho líquido fornecido ao ciclo e de 22 kJ. Considerando que o refrigerante muda de vapor saturado para líquido saturado durante o processo de rejeição de calor, determine a pressão mínima do ciclo.
Passo 1
Vamos lá! A questão nos informa que um ciclo de refrigeração Carnot é executado num sistema fechado com uma massa fixa de R-134a. A entrada líquida de trabalho e o são dadas as temperaturas máximas e mínimas. A pressão mínima no ciclo deve ser determinada.
Então podemos representar como:
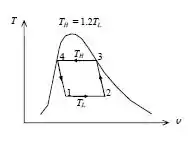
Vamos supor que a geladeira opera no ciclo inverso do Carnot, que é totalmente reversível.
Passo 2
Pronto já temos todas as informações necessárias, vamos para a análise. O coeficiente de desempenho do ciclo é
Como também,
Logo,
Desse modo,
Passo 3
Já que a entalpia de vaporização a um dado T ou P representa a quantidade de transferência de calor por unidade de massa como uma substância é convertido de líquido saturado para vapor saturado a esse T ou P. Portanto, é a temperatura que corresponde ao
de 137,5 kJ/kg, e é determinado a partir das tabelas R-134a a ser
Então
Portanto,