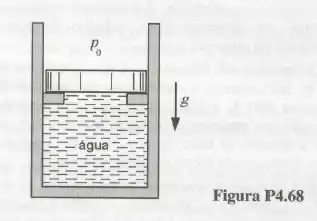
Considere o conjunto cilindro-pistão mostrado na Fig. P4.68. O conjunto contém de água. Inicialmente, a água se encontra no estado saturado em que a pressão é e o título é . A água é então aquecida até o volume interno do conjunto se tornar igual ao triplo do volume interno inicial. A massa do pistão é tal que a pressão interna necessária para desencosta-lo do esbarro é . Nestas condições. Determine a temperatura e o volume da água no estado final do processo e, também, o trabalho realizado pela água no processo.

Galera para determinar o volume específico de uma mistura, que é caso do volume inicial, a fórmula do volume específico médio é:

Temos que encontrar o volume específico da fase líquida e da fase líquida e vapor.

Como? Vamos olhar com as condições de estado na tabala que resulta nos seguintes volumes:

E

A diferença entre os volumes configura no volume da fase líquida vapor.

Vamos aplicar a fórmula do volume:

Utilizando a relação que o volume final é o triplo do inicial:

Multiplicando pela massa o volume específico, o volume final é:

Para o cálculo do trabalho nós temos um processo que o volume é constante até o momento em que a pressão consegue chegar na pressão mínima para levantar o pistão.

Este gráfico vai ilustrar melhor:

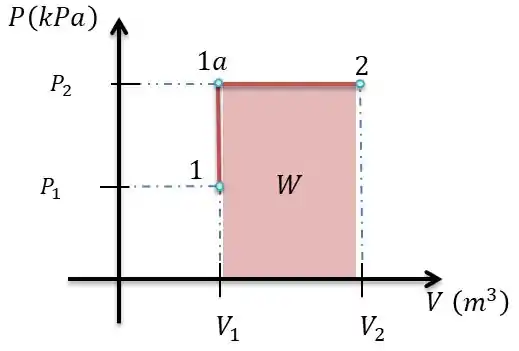
Note que o trabalho é a área integral que se da pela área sobe a função, portanto:

Estamos multiplicando pela massa, por causa do volume específico.

Fecho galera, valeu.