Considere um motor térmico de Carnot que utiliza amônia como fluido de trabalho. A temperatura do reservatório térmico onde se transfere é . Neste processo de transferência de calor, a amônia se transforma de líquido saturado em vapor saturado. Sabendo que a pressão na amônia é igual a no processo de rejeição de calor, determine , a eficiência do ciclo, o calor transferido no ciclo, por quilograma de amônia, e a entropia da amônia no início da rejeição de calor para a fonte fria.
Passo 1
Opa, tudo bem?
Vem comigo resolver uma questão de termodinâmica?
Então borá lá!
Começamos o problema desenhando um ciclo de Carnot para facilitar nossa visualização e entendimento do sistema proposto:
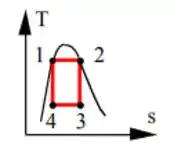
Passo 2
Começando a resolver nosso problema, primeiramente iremos determinar .
Analisando o ciclo construído, sabemos que:
Conseguimos obter com a seguinte informação:
“a pressão na amônia é igual a no processo de rejeição de calor”
Que nos indica que:
Na Tabela B.2.1, obtemos o valor de:
Passo 3
Seguindo, calcularemos a eficiência do ciclo:
Dados:
;
.
Temos:
Passo 4
Agora, calcularemos o calor transferido no ciclo da seguinte forma para T constante (60°C):
Integrando, obtemos:
Modificando a equação, concluímos que:
Assim:
Na Tabela B.2.1, o valor da entalpia de evaporação para a amônia saturada a 60°C é de:
Passo 5
Temos que o início rejeição de calor para a fonte fria acontece no Ponto 3, como podemos ver no ciclo do Passo 1, a entropia do Ponto 3 é semelhante a entropia no Ponto 2, desse modo a entropia da amônia nesses pontos é dada por:
Conseguimos chegar até o nosso resultado!
Até logo!