Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 3.Problemas - Ex. 116
Considere o refrigerante como fluido de trabalho. Determine a pressão e a temperatura de saturação para estado onde o volume específico do vapor saturado é igual a .
Passo 1
Fala pessoal, tudo bem? Vem comigo que vai da tudo certo.
Temos o refrigerante e temos volume específico do vapor saturado é igual a .
Olhando na tabela .
Note que temos dois candidatos interessantes para escolha estamos em .
Teremos que interpolar os dados para chegarmos aproximadamente na temperatura e pressão desejada.
Passo 2
O método de interpolação consiste em criarmos um gráfico de reta com os dados que desejamos e assim podemos calcular a pressão e a temperatura.
Vai ficar mais claro, na prática!
Para, temos:
Para :
Montando o gráfico, irei montar o gráfico com o eixo y negativo para cima só para fica mais bonitinho mesmo:
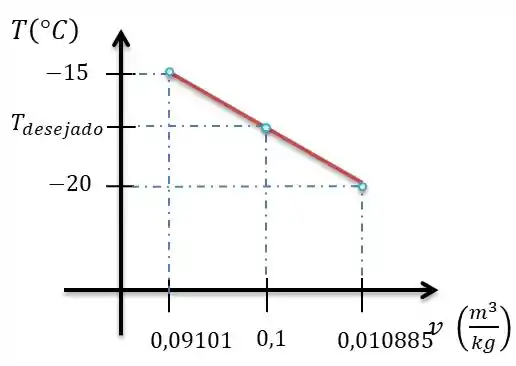
Ficou mais claro agora né! Bem como se trata de uma equação de reta, basta calcularmos a nossa temperatura desejada.
Passo 3
Utilizarei dois pontos e :
Substituindo:
O coeficiente angular pode ser determinado por:
Escolhendo 2 pontos que conhecemos e , fica:
Substituindo no cálculo da temperatura e isolando a temperatura desejada, temos:
Passo 4
Agora que já sabemos como funciona uma interpolação, partiu replicar os passos para a pressão.
Para , temos:
Para :
Montando o gráfico:
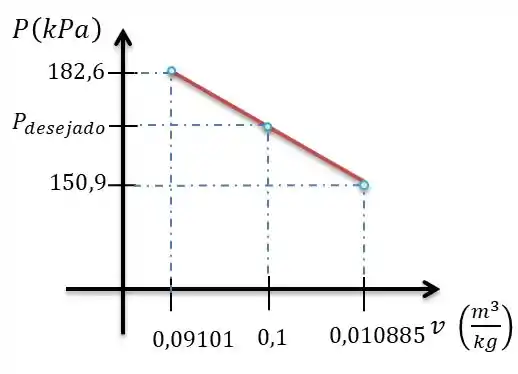
Passo 5
Utilizarei dois pontos e :
Substituindo:
O coeficiente angular pode ser determinado por:
Escolhendo 2 pontos que conhecemos e , fica:
Substituindo no cálculo da pressão e isolando a pressão desejada, temos:
É isso ae pessoal! Valeu.