Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 2.Problemas - Ex. 17
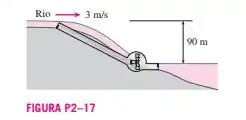
Considere um rio escoando em direção a um lago com uma velocidade média de 3 m/s a uma vazão de 500 em um local 90 m acima da superfície do lado. Determine a energia mecânica total da água do rio por unidade de massa e o potencial para geração de potência do rio naquele local.
Passo 1
Olá, pessoal! Esse problema é sobre um rio que é usado para produzir energia elétrica, extraindo a energia mecânica da água.
Estão prontos para fazer uma questão de energia mecânica?
A questão pede que a gente calcule dois termos. Primeiro, ela quer que a gente calcule a energia mecânica total por unidade de massa presente na água do rio. Depois ela quer que a gente calcule o potencial para geração de potência do rio (essa potência é representada por . Ela é a taxa de energia elétrica que pode ser produzida através do rio). Ou seja, ela quer saber quanto de energia disponível tem no rio que pode ser convertida para eletricidade.
A figura abaixo mostra todos os dados que temos para calcular e .
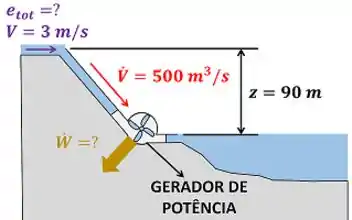
é a velocidade média da água do rio, quando ela está a uma altitude . é a vazão volumétrica de água do rio. Traduzindo, é o volume de água que passa pelo rio a cada segundo.
Para calcular e temos que lembrar de dois fatos. A energia total por unidade de massa do rio é a soma da energia cinética por unidade de massa com a energia potencial por unidade de massa da água .
Além disso, Como o gerador usa a energia da água para gerar eletricidade, a taxa máxima de energia elétrica que ele pode produzir é igual a taxa de energia total presente na água.
Passo 2
Nesse passo, vamos calcular a energia total por unidade de massa do rio .
Ela é a soma de duas parcelas. Uma parcela é a energia cinética por unidade de massa da água . A outra parcela é a energia potencial por unidade de massa da água .
Como a energia cinética por unidade de massa da água só existe por causa do movimento da água, podemos dizer que depende da velocidade da água. A fórmula de em função da velocidade se encontra abaixo. Como já conhecemos , podemos calcular .
Como a energia potencial por unidade de massa da água só existe por causa da altitude da água, podemos dizer que depende da altitude da água. A fórmula de em função da altitude se encontra abaixo. A letra presente na fórmula abaixo é a aceleração da gravidade. Como já conhecemos e , podemos calcular .
Somando as duas parcelas e encontramos a energia total por unidade de massa .
Passo 3
Neste passo, vamos calcular o valor da taxa máxima de energia elétrica que pode ser produzida através da água do rio.
calculada no passo anterior é a energia contida em cada quilograma da água no rio. A taxa de energia total da água que passa pelo rio é igual a energia por quilograma da água multiplicada pela massa de água que passa a cada segundo pelo rio .
também é conhecida como a vazão mássica. Ela pode ser obtida a partir da vazão volumétrica , multiplicando pela densidade da água.
A densidade da água não está presente no enunciado. No entanto, a água líquida a temperatura ambiente tem uma densidade que vale aproximadamente .
Substituindo esse valor na fórmula de , encontramos:
Como o gerador usa a energia da água para gerar eletricidade, a taxa máxima de energia elétrica que ele pode produzir é igual à taxa de energia total presente na água.
Convertendo esse valor em watt para um valor em megawatt , encontramos: