Enunciado
Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 11.Problemas - Ex. 87
Considere um sistema de loop duplo, constituído de um ciclo de refrigeração, acionado por um ciclo de potência acoplado, ambos ideais e usando o R-12 como fluido de trabalho, conforme mostrado na Fig. P11.87. Vapor saturado a sai da caldeira e é expandido na turbina até a pressão no condensador. Vapor saturado a sai do evaporador e é comprimido até a pressão de condensação. A razão entre as vazões mássicas nos loops é tal que a turbina produz exatamente a potência necessária para acionar o compressor. As duas correntes, saindo da turbina e do compressor, se misturam e entram no condensador. O líquido saturado, saindo do condensador a , é então separado em duas correntes nas proporções necessárias. Determine a razão entre as vazões mássicas no loop de potência e no loop de refrigeração. Determine também o coeficiente de performance do ciclo em termos da razão .
Passo 1
Fala, galera! Vamos resolver essa questão.
Essa questão é basicamente aplicação de fórmulas e nós vamos relembrando essas fórmulas nos próximos passos. Vamos começar dando uma olhadinha nos diagramas do processo:
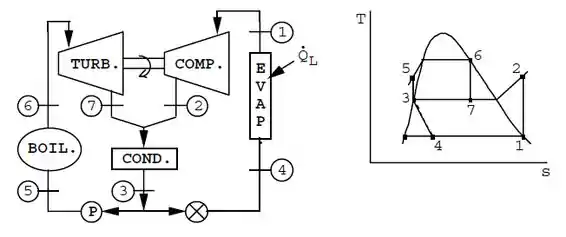
Pela Tabela B.3.1, temos:
Implica que,
E,
Que nos dá a pressão:
Logo,
Vamos lá!
Passo 2
Vamos primeiro para a turbina. Note que:
Como também,
Já para o compressor, temos tabelas computadorizadas para o devido valor de que nos fornecem a entropia:
E implica:
Agora para a turbina mais o compressor, temos pela equação da continuidade:
E pela equação de energia:
Portanto,
Passo 3
Agora vamos analisar a bomba. Note que,
Para o evaporador:
Para a caldeira:
Portanto, teremos que:
E finalizamos a questão! Até a próxima, galera!