Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Termodinamica,Teoria Cinética e Termodinâmica Estatística, Sears e Salinger- Ed: 3º - Capítulo 3.Problemas - Ex. 6

Um gás ideal e um bloco de cobre tem volume iguais de 0.5   m 3 a 300 K e a pressão atmosférica. A pressão em ambos é aumentada reversível e isotermicamente para 5 atm. (a) Explique, com ajuda de um diagrama P - V por que o trabalho não é o mesmo nos dois processos. (b) em qual dos processos o trabalho realizado é maior? (c) Encontre o trabalho feito sobre cada um, se a compreensibilidade do cobre é 0.7 × 10 - 6   a t m - 1 . (d) Calcule a variação de volume em cada caso.

Passo 1

(a)

Opaaaa, beleza? Nesta parte da questão vamos discutir por que o trabalho não é o mesmo nos dois processos.

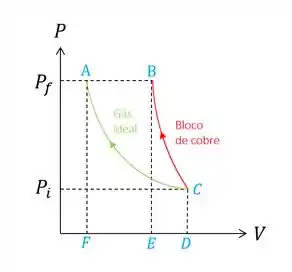
Se damos uma olhada na Figura, vemos que a área abaixo da curva que representa o trabalho feito para cada material, é diferente, é por isso que o trabalho não é o mesmo.

Passo 2

(b) Para o gás ideal a área é maior (Area ACDFA) do que para o bloco de cobre (Área BCDEV), e como consequência o trabalho é maior.

Passo 3

(c) Para resolver a terceira parte de nosso problema, temos os seguintes dados:

P i = 1   a t m = 1.013 × 10 5   P a

P f = 5   a t m = 5 × 1.013 × 10 5   P a

β = 0.7 × 10 - 6   a t m - 1 = 0.7 × 10 - 6   1.013 × 10 5   P a

V i = 0.5   m 3

Onde β é o coeficiente de compreensibilidade.

Temos então para o cobre que o trabalho é:

W c = - V β 2 ( P f 2 - P i 2 )

W c = - 0.5 2 0.7 × 10 - 6   1.013 × 10 5   P a 5 2 - 1 2 1.013 × 10 5   P a 2

W c = - 0.35 × 10 - 6 2 ( 24 ) ( 1.013 × 10 5   P a )

W c = - 0.42   J

Para o gás ideal temos:

W g = n R T ln ⁡ P i P f

Lembrando da equação dos gases ideais P V = n R T

W g = P i V i ln ⁡ P i P f

W g = 1.013 × 10 5   × 0.5 ln ⁡ 1 5

W g = - 81518,03   J

O signo negativo para os dois casos indica que o trabalho é feito no sistema, em outras palavras, o volume diminui.

(d)

Para o caso do gás ideal:

P i V i = P f V f

Isolando V

V f = P i V i P f = 0.5 5 m 3 = 0.1   m 3

Então a variação do volume para o gás ideal é:

∆ V = V f - V i = 0.1 - 0.5 = - 0.4   m 3

Para o cobre, por definição do coeficiente de compreensibilidade:

β = - 1 V d V d P

β d P = - d V V

β ∫ P i P f d P = - ∫ V i V c d V V

β P f - P i = ‎   ‎   ‎   - ln ⁡ V ‎   ‎   V i V c

β P f - P i = - ln ⁡ V c + ln ⁡ V i

ln ⁡ V c - ln ⁡ V i = - β P f - P i

ln ⁡ V c V i = - β P f - P i

e ln ⁡ V c V i = e - β P f - P i

V c V i = e - β P f - P i

V c = V i e - β P f - P i

Então a variação do volume do cobre é:

∆ V c = V c - V i

∆ V c = V i e - β P f - P i - V i

∆ V c = V i ( e - β P f - P i - 1 )

∆ V c = ( 0.5 ) ( e - 0.7 × 10 - 6   ( 1.013 × 10 5   ) 5 - 1 1.013 × 10 5 - 1 )

∆ V c = ( 0.5 ) ( e - 2.8 × 10 - 6 - 1 )

∆ V c = - 1.4 × 10 - 6 m 3

Resposta

Resposta nos passos

Exercícios de Livros Relacionados

Com sidere um processo politrópico onde a pressão é diretamente proporcional ao volume n = - 1 . Observe que este processo pode ser realizado no arranjo mostrado na Fig. P 2.83 . O estado inicial do p
Um conjunto cilindro-pistão contém, inicialmente, 0,1m 3 de um gás a 1M P a e 500 ° C . O gás é então expandido num processo onde p V = c t e . Admitindo que a pressão final seja igual a 100k P a , de
Um conjunto cilindro-pistão contém 0,1k g de ar. Inicialmente, a temperatura e a pressão são iguais a 400K e 100k P a . O ar é comprimido, segundo um processo politrópico com n = 1,3 , até que a press
Determine o trabalho realizado no processo descrito no Prob. 3.106.
Considere um arranjo cilindro-pistão que inicialmente contém 0,5k g de vapor saturado de 4 - 134 a a - 10 ° C . O refrigerante é então comprimido até que a pressão atinja 500k P a num processo politró