Enunciado
Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 9.Problemas - Ex. 19
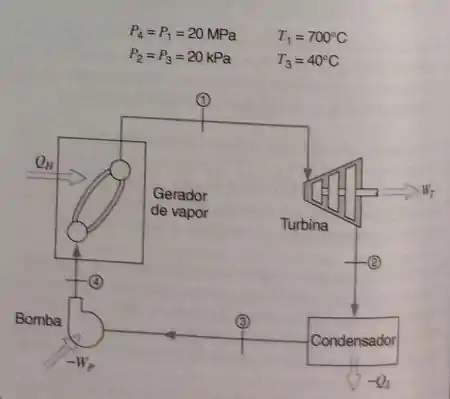
Considere uma turbina a vapor de uma planta de potência, operando perto da pressão crítica, como mostrado na Fig. P9.19. Como uma primeira aproximação, pode-se supor que a turbina e os processos de bombeamento são reversíveis e adiabáticos. Desprezando variações nas energias cinética e potencial, calcule
a. O trabalho específico da turbina e o estado termodinâmico na saída da turbina.
b. O trabalho na bomba e a entalpia do estado na saída da bomba.
c. O rendimento térmico do ciclo.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Primeiramente, recebemos os seguintes dados para usina de turbina a vapor com turbina e bomba sendo adiabáticas:
A – Da tabela da água superaquecida B.1.3. correspondente a e , podemos encontrar a entropia e a entalpia específicas do estágio 1:
Não há mudança na entropia no processo adiabático, logo
Da tabela de água saturada B.1.2, com os valores correspondentes a , podemos encontrar a entalpia e a entropia específicas de saturação e evaporação:
Calculando o fator de qualidade do estágio 2:
Fazendo a substituição de valores,
Calculando a entalpia específica do estágio 2:
E calculando a saída de trabalho específica da turbina:
Passo 2
B – Da tabela de água saturada B.1.1. correspondente a , podemos encontrar entalpia e volume específicos:
Calculando a entrada de trabalho da bomba:
E com isso, calculando a entalpia da bomba de saída:
Passo 3
C – Por fim, calculando a eficiência térmica
Substituindo os valores,