Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 10.Problemas - Ex. 77
Considere uma usina de cogeração modificada com regeneração. O vapor entra na turbina a 9 MPa e 400 °C e se expande até uma pressão de 1,6 MPa. Nessa pressão, 35% do vapor é extraído da turbina, e o restante se expande até 10 kPa. Parte do vapor extraído é usado para aquecer a água de alimentação em um aquecedor de água de alimentação aberto. O restante do vapor extraído é usado para aquecimento e deixa a unidade de processamento térmico como líquido saturado a 1,6 MPa. Em seguida, ele é misturado à água de alimentação que deixa o aquecedor de água de alimentação, e a mistura é bombeada até a pressão da caldeira. Considerando que as turbinas e bombas sejam isentrópicas, mostre o ciclo em um diagrama T-s que inclua as linhas de saturação e determine o fluxo de massa de vapor na caldeira para uma potência líquida de 25 MW.
Passo 1
O que devemos fazer primeiro é pegar as propriedades do fluido nos pontos de interesse com os dados fornecidos no enunciado, então, com a ajuda das tabelas termodinâmicas do apêndice A, temos:
Com esse valor, podemos encontrar o trabalho específico exigido pela bomba 1 e depois encontrar a entalpia no ponto 2, então teremos:
E, aplicando o equilíbrio de energia específica para a bomba 1, temos:
Agora, continuando com as propriedades, temos:
Com esse valor, podemos encontrar o trabalho específico exigido pela bomba 2 e depois encontrar a entalpia no ponto 5, então teremos:
E, aplicando o equilíbrio de energia específica para a bomba 2, temos:
E, para o ponto 6, teremos:
Passo 2
Agora, dando continuidade as propriedades no ponto de interesse, temos:
Com esses dois valores, podemos encontrar o título no ponto 7 através de:
E, com esse título, podemos encontrar a entalpia no ponto 7, que será:
Agora, para o ponto 8, teremos:
E, da mesma forma, com esses valores, podemos encontrar o título no ponto 8, então, teremos:
E, com o valor do título, encontrar a entalpia no ponto 8:
E, com todos os pontos, podemos plotar o diagrama T-s para o sistema, que será:
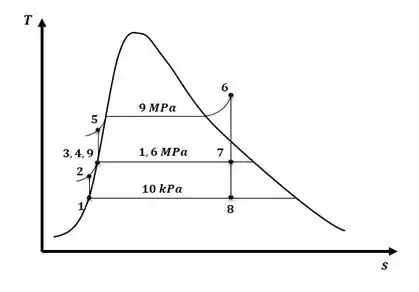
Passo 3
Beleza! Agora que temos todas as propriedades, vamos começar análise de fato. Então, chamando a fração mássica que vai para o regenerador de , podemos escrever o trabalho específico gerado pela turbina com o auxílio da equação 10-28 apresentada nessa seção como:
Substituindo os valores conhecidos, temos:
E o trabalho específico demandado pelas bombas em função da vazão na caldeira, será:
Substituindo os valores conhecidos:
Dessa forma, o trabalho líquido, que é a diferença entre o trabalho produzido pela turbina e o trabalho consumido pelas bombas será:
E, com isso, podemos calcular a vazão mássica em função da potência líquida fornecida no enunciado, então, teremos: