Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 16.Problemas - Ex. 88
Determine a constante de equilíbrio da reação , a qual ocorre a 690 kPa e 3000 K. Os logarítmos naturais da constante de equilíbrio das reações e a 3000 K são 9,685 e 15,869, respectivamente.
Passo 1
Tá legal! A primeira coisa que devemos fazer é escrever as duas equações de dissociação:
Somando essas duas equações, só lembrando que para o teremos a dissociação e para o a formação, chegamos em:
Então, cancelando o carbono que aparece dos dois lados, chegamos em:
Passo 2
Então, como somamos as equações de dissociação, no entanto, invertendo a ordem de , então, podemos somar os valores de fornecidos, mas lembrando de usar o sinal negativo para o termo do , então o novo será:
E, agora, inclundo a dissociação da água na equação, temos:
Consultando a tabela A-28 do apêndice A, para obter o valor de teremos:
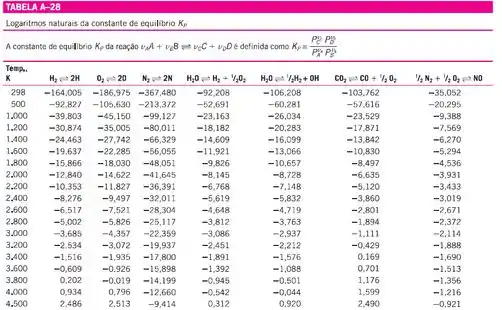
No nosso caso, estamos formando 2 mol de , então devemos multiplicar o valor tabelado por 2, dessa forma, temos:
Passo 3
Agora, somando as equações do passo 2 para formar a equação fornecida no enunciado, temos:
Então, somando os valores de do passo 2, temos: