Quando dobramos a razão de compressão de um ciclo Otto ideal, o que acontece com a temperatura máxima e pressão do gás quando o estado do ar no inicio da compressão e a quantidade de calor adicionado permanecem os mesmos? Considere calores específicos constantes à temperatura ambiente.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O ciclo Otto pode ser representado pelo seguinte diagrama :
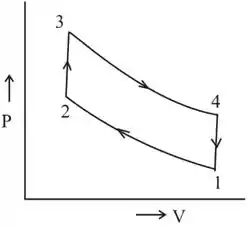
Para uma taxa de compressão , temos que:
Se a taxa de compressão dobrar, temos que:
Como para o processo isentrópico , temos que:
E:
Passo 2
Como queremos saber o que acontece com a temperatura e pressão máxima do ciclo, temos que analisar o estado que é onde ocorre a temperatura e pressão máxima.
A quantidade de calor que entra no processo não tem relação com a taxa de compressão. Logo:
Portanto... Quando a taxa de compressão é , temos que:
Quando a taxa dobra, temos que:
Observe que o termo com a taxa de compressão dobrada será maior, portanto, podemos dizer que uma maior taxa de compressão aumenta a temperatura máxima do ciclo.
Passo 3
Agora vamos analisar o que ocorre com a pressão:
O menor volume específico de gás é obtido no estado :
Quando dobramos a taxa de compressão, temos que:
Aplicando na equação do gás ideal no estado , temos que:
Substituindo os termos, temos que:
Analogamente, para o dobro da taxa de compressão, teremos que:
Podemos observar que quanto maior a taxa de compressão, maior será a pressão máxima no ciclo.
Resposta
O aumento da taxa de compressão, ocasiona o aumento da temperatura máxima e da pressão máxima no ciclo.