Escrevendo as equações da primeira e da segunda lei (e simplificando), obtenha uma expressão para o trabalho reversível de um sistema com escoamento em regime permanente que troca calor com a vizinhança a na quantidade e também com um reservatório térmico a a uma taxa . (Dica: elimine entre as duas equações.)
Passo 1
Vamos lá! Para responder à questão, observe que escrevendo balanços de energia e entropia, uma relação para o trabalho reversível deve ser obtida para um sistema de fluxo constante que troca calor com o ambiente em a uma taxa de assim como um reservatório de calor a temperatura na quantidade .
Podemos representar como,

Passo 2
Certo! Agora tomamos a direção da transferência de calor para o sistema (entrada de calor) e a direção da transferência de trabalho para ser do sistema (saída de trabalho). O resultado obtido ainda é geral, uma vez que quantidades com direções opostas podem ser manipuladas a da mesma forma, usando sinais negativos. A energia e os equilíbrios de entropia para este sistema fechado estacionário podem ser expressos como
Balanço energético
![]()
![]()
ou,
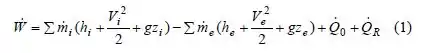
Balanço de entropia:
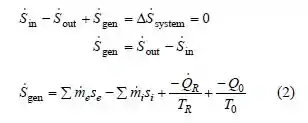
Passo 3
Estamos quase terminando! Agora vamos resolver para a partir de (2) e substituindo em (1) rendimentos

Em seguida, a relação de trabalho reversível é obtida pela substituição de = 0,

Um resultado positivo para indica saída de trabalho, e um resultado negativo, entrada de trabalho. Além disso, o é uma quantidade positiva para transferência de calor para o sistema, e uma quantidade negativa para transferência de calor do sistema.
Resposta
Ei, a resposta está no passo a passo :)