Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 8.Problemas - Ex. 35

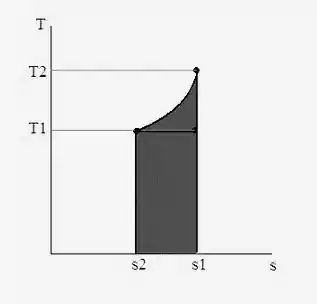
Para os estados e processos do Problema 8.34, estime a transferência de calor por unidade de massa pela área no diagrama T-s e compare com o valor correto.

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Recebemos os seguintes dados para a água em um tanque rígido:

T 1 = 250 ° C

P 1 = 1000   k P a

Da tabela de água superaquecida B.1.3, com valores correspondentes a T 1 = 250 ° C e P 1 = 1000   k P a , nós podemos encontrar o volume específico, a entropia e a energia interna:

u 1 = 2709,9 k J k g

v 1 = 0,23268 m 3 k g

s 1 = 6,9246 k J k g   K

A água está no tanque rígido, então não há mudança no volume específico:

v 2 = v 1 = 0,23268 m 3 k g

Da tabela de água saturada B.1.1, com valores correspondentes a T = 170 ° C , nós podemos encontrar o volume específico e a energia interna:

u = 2570,46 k J k g

s = 6,6663 k J k g   K

v = 0,24283 m 3 k g

Para o caso de T = 175 ° C

u = 2580,19 k J k g

s = 6,6256 k J k g   K

v = 0,2168 m 3 k g

Passo 2

Calculando a energia interna específica final, entropia e temperatura usando o método de interpolação linear:

u 2 = 2570,46 + 0,23268 - 0,24283 0,2168 - 0,24283 ∙ 2580,19 - 2570,46 = 2577,9 k J k g

Para o caso da temperatura T 2

T 2 = 170 + 0,23268 - 0,24283 0,2168 - 0,24283 ∙ 175 - 170 = 172 ° C

E

s 2 = 0,6663 + 0,23268 - 0,24283 0,2168 - 0,24283 ∙ 6,6256 - 6,6663 = 6,6504 k J k g

A transferência de calor específico é igual a:

q = u 2 - u 1 = 2577,9 - 2709,9 = - 132 k J k g

Vamos calcular agora a transferência de calor específica usando a equação de entropia:

q = ∫ T ∙ d s = 1 2 ∙ T 1 - T 2 ∙ s 2 - s 1 + s 2 - s 1 ∙ T 2

Novamente, fazendo o processo de substituição

q = 1 2 ∙ 250 - 172 ∙ 6,6504 - 6,9246 + 6,6504 - 6,9246 ∙ 172 + 273 = - 132,7 k J k g

A transferência de calor específica calculada a partir da equação de entropia é a mesma que a transferência de calor calculada pela equação de energia.

Passo 3

O diagrama T-s é igual a

Resposta

q = - 132,7 k J k g

Exercícios de Livros Relacionados

Mostre que ∂ s / ∂ T x0 para todos os processos em que x é uma propriedade intensiva ou extensiva arbitrária do sistema.
Uma massa m de um líquido a uma temperatura T 1 é misturada com uma massa igual do mesmo líquido a uma temperatura T 2 . O sistema está termicamente isolado. Mostre que a variação de entropia do unive
Um mol de um gás monoatômico, inicialmente à temperatura T i , expande-se adiabaticamente contra um embolo sem massa, até que seu volume dobre. A expansão não é necessariamente quase estática ou rever
Vapor d’agua saturado 150° C é expandido até uma pressão mais baixa, a temperatura constante. Determine as variações de u em s quando a pressão final for: a .100K P ab . 50 K P ac .10 K P a
Determine a entropia para os seguintes estados da água e indique cada estado em relação à região bifásica num diagrama T-s. a .250° C ,v=0,02 m ³ / K g ³ b .250° C ,2000K P a c .- 2° C ,100K P a d .20