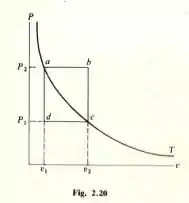
Na Fig. 2.20, seja , , . Encontre (a) a temperatura T, (b) O volume especifico , (c) a temperatura nos pontos e , (d) O volume no ponto se o sistema consistir de de hidrogênio, (e) a massa do hidrogênio.
Passo 1
Fala, galerinha. Estamos aqui pra mais um exercício, mas calma que vou te ajudar nessa.
Nessa questão temos que tirar a informação do gráfico e depois substituir nas equações para encontrar o que precisamos.
Passo 2
Primeiro queremos qual é a temperatura T. Temos a relação que vale pra qualquer gás ideal, que é
Isolando nessa equação, temos
A pressão no ponto é , o volume molar é . Substituindo os valores temos
Passo 3
Para o volume específico temos que
Isolando temos
Passo 4
Para a temperatura nos pontos e , fazemos o mesmo raciocínio que estamos fazendo, usando a lei dos gases ideais e achando o que queremos. Então, para o ponto temos
Isolando temos
E para o ponto temos
Novamente isolando temperatura, temos
Passo 5
Para encontrar o volume dessa quantidade de hidrogênio, só temos que multiplicar esse valor pelo volume específico que foi dado no enunciado. Então vamos ter
Onde é o volume que temos, é o volume específico e é o número de quilomoles que temos do elemento. Substituindo os valores que temos
Passo 6
O último passo é encontrarmos qual a massa do hidrogênio que temos nesse volume. Pra isso, precisamos lembrar da massa molar do hidrogênio que é
Como temos vamos ter
Mais um problema feito. Bora pra mais um?
Resposta
Resposta nos passos