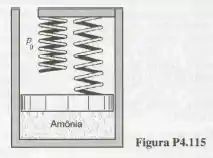
A Fig mostra um conjunta cilindro-pistão que contém amônia a , e . A massa do pistão pode ser considerada nula, as duas molas são lineares e apresentam a mesma constante de mola. As duas molas estão distendidas quando o pistão se encontra no fundo do cilindro e a segunda mola toca o pistão quando o volume confinado for igual a . A amônia é, então, aquecida até que a pressão interna se torne igual a . Sabendo que a pressão atmosférica é , determine o valor da pressão na amônia no momento em que o pistão toca a segunda mola. Calcule, também, a temperatura final do processo e o trabalho realizado pela amônia.
Passo 1
Oi meu povo, tudo bem? Vamos analisar direitinho essa questão.
Primeiro vamos entender o enunciado. Nosso sistema tem a configuração mostrada na Figura e o exercício quer saber o valor da pressão na amônia no momento em que o pistão toca a segunda mola.
Também queremos a temperatura final do processo e o trabalho realizado pela amônia.
Bom... Nos é dito que a amônia está sendo aquecida até uma pressão de então o final do processo está relacionado à essa pressão.
Vamos fazer o seguinte então... Considerando que teremos quatro momentos no nosso sistema, vamos propor que o momento inicial, quando o pistão está na parte inferior do cilindro, seja o .
Quando o volume de amônia na câmara for igual a , estaremos no . Quando o pistão atingir a segunda mola e o volume de amônia na câmara for estaremos no .
E finalmente, quando atingirmos nossa pressão final de , estaremos no .
Passo 2
No , teremos que o pistão está encostado no fundo do cilindro, portanto a única pressão agindo no pistão será a atmosférica. Logo:
No estado , nos é dito que a temperatura da amônia na câmara é de . Analisando a tabela de propriedades para a amônia, não temos valores de pressão ou volume específico para esta temperatura, portanto, teremos que interpolar os valores entre e .
Resolvendo, teremos que:
O exercício nos diz que teremos no Estado 1, portanto, temos que encontrar e correspondentes à , para podermos descobrir o volume específico. Temos que:
Resolvendo, temos que:
Temos também que:
Resolvendo, temos que:
Nosso volume específico será:
Passo 3
Como sabemos que o volume no Estado 1 é de e descobrimos o volume específico também nesse estado, podemos então descobrir a massa de amônia no nosso sistema.
Temos que:
A massa de amoníaco no sistema é de:
Bom, analisando o sistema, podemos dizer que ele terá um comportamento constante até atingir a segunda mola, então podemos encontrar a pressão no estado considerando que o sistema é linear até esse ponto, como mostrado no diagrama abaixo:

Teremos que:
Substituindo os valores, teremos que:
A pressão quando o pistão atinge a segunda mola, será de:
Passo 4
Como a constante da mola é a mesma para as duas molas, podemos dizer que quando as duas molas estão em contato com o pistão, a constante da mola equivalente será o dobro da constante da mola inicial.
Por isso no nosso esboço do diagrama , a inclinação mudou. Temos que a inclinação da linha do Estado 2 ao Estado 3, será duas vezes a inclinação inicial. Ou seja:
Como sabemos que:
Teremos que:
Resolvendo, teremos que:
Passo 5
Como sabemos a massa de amônia, podemos descobrir o volume específico neste estado:
Para uma pressão de e um volume específico de , analisando a tabela, temos amônia superaquecida. Portanto, interpolando, podemos encontrar a temperatura neste estado:
Resolvendo, teremos que a temperatura final do sistema é de:
O exercício também nos pede para calcular o trabalho feito pela amônia. Temos que:
Substituindo os dados, temos que:
O trabalho total realizado pela amônia será: