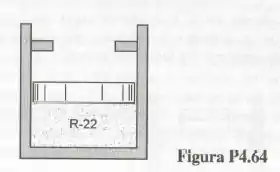
A Fig. P4.64 mostra um conjunto cilindro-pistão que contém refrigerante . Quando o pistão está encostado nos esbarros, o volume da câmara é igual a . No estado inicial a temperatura é , a pressão é e o volume da câmara é igual . O sistema é então aquecido até que a temperatura atinja . Pergunta-se:
a) O pistão está encostado nos esbarros no estado final?
b) Qual é o trabalho realizado neste processo?
Passo 1
Fala pessoal, tudo bem?
Irei ilustrar a situação:
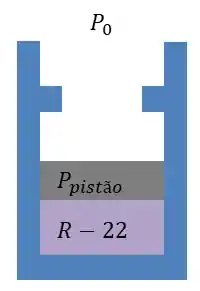
Para determinarmos a letra (a) teremos que saber se a pressão final é maior que a pressão inicial , pois, se com o pistão não encosta nos esbarros se o nosso pistão ira se mover para cima, então bora calcular essa pressão.
Queremos calcular o trabalho realizado durante o processo, como o trabalho pode ser calculado pela área integrável do diagrama , iremos desenhar para entender que tipo de área temos.
Passo 2
a) Galera como o nosso sistema trabalha com a pressão é constante durante o processo, temos o seguinte diagrama:
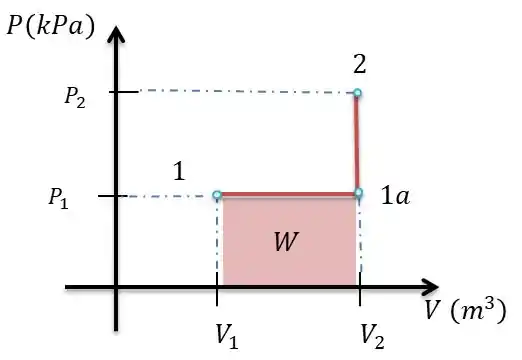
Do ponto 1 ao ponto 1a o processo é de expansão, pois, a nossa temperatura está aumentando a pressão está constante, portanto, o resultado é que o nosso volume irá aumentar.
Quando o pistão chega em este é o momento em que o pistão encosta nos esbarros.
Sobe este momento que iremos fazer a análise de que se a temperatura for menor que isso significa que .
Passo 3
Para encontrar esta análise teremos que utilizar as tabelas de estado, para isso precisamos de mais uma condição de estado além da temperatura, vamos calcular o volume específico:
Determinando a massa:
Olhando na tabela com as condições de estado inicial, temos:
Substituindo no calculo da massa e convertendo :
Com a massa em mãos podemos determinar :
Com e , olhando na tabela temos que a temperatura é :
Se isso implica que . O pistão no estado final está encostando nos esbarros.
Passo 4
Bem galera como foi dito anteriormente o trabalho é a área integrável de baixo da função no diagrama , como ficou bem ilustrado no diagrama.
Temos que o trabalho é:
É isso galera.