Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 11.Problemas - Ex. 31
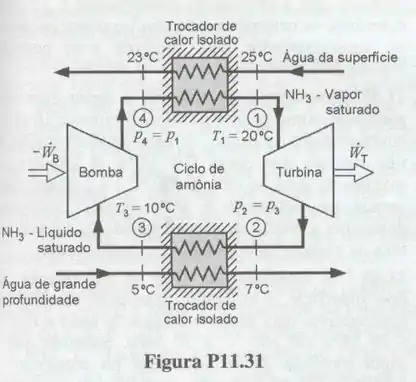
A Fig. P11.31 mostra um ciclo de potência Rankine que utiliza amônia como fluido de trabalho e que foi projetado para operar a partir da diferença de temperaturas existente na água dos oceanos. Admitindo que a temperatura superficial da água é igual a , que a temperatura numa certa profundidade é igual a e que a vazão de amônia no ciclo é , determine:
a) A potência desenvolvida na turbina e a consumida na bomba.
b) A vazão em massa de água através de cada trocador de calor.
c) O rendimento térmico deste ciclo.
Passo 1
Bora resolver essa questão comigo?
Vamos lá!
As propriedades desta questão foram obtidas da Tabela B.2.
Letra a)
Começamos o problema analisando a turbina.
Aqui, assumimos um processo adiabático e reversível, ou seja, isentrópico, então:
Assim:
Aplicando a equação de energia, temos:
Assim, sua potência se dá:
Agora, analisando a bomba.
Considerando um processo isentrópico e incompressível, facilmente calculamos seu trabalho:
Desse modo, calculando a sua potência:
Passo 2
Letra b)
Calculando a vazão em massa de água através de cada trocador de calor.
Considerando o trocador de calor com a menor temperatura de água:
Assim:
Agora, considerando o trocador de calor com a menor temperatura de água:
Assim:
Passo 3
Letra c)
Por fim, vamos determinar o rendimento térmico deste ciclo:
Te espero na próxima questão!
Resposta
a) .
b) .
c) .