Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 13.Problemas - Ex. 85
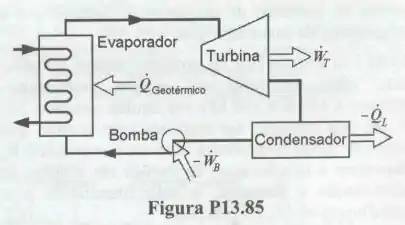
A Fig. P13.85 mostra o esquema do ciclo térmico utilizado no aproveitamento do calor fornecido por uma fonte geotérmica. O fluido de trabalho do ciclo é o isobutano e o fluido entra na turbina, que pode ser modelada como adiabática reversível, a e . O fluido deixa o condensador com líquido saturado a . As propriedades termodinâmicas do isobutano são: , , , e massa molecular igual a Nestas condições, determine os trabalhos específicos na turbina e na bomba.
Passo 1
Vem comigo resolver essa questão?
Se ajeita ai e bora lá!
Começamos o nosso problema expondo algumas informações do nosso processo:
Pelas tabelas de Apêndice A, temos:
Assim, temos:
Passo 2
Pela Fig. D.1, obtemos:
Assim:
Passo 3
Pela Fig. D.2, obtemos:
Além disso:
E
Passo 4
Pela Fig. D.3, obtemos:
Além disso:
E
Passo 5
Como possuímos um sistema adiabático e reversível, temos que:
Então conseguimos calcular o título a partir disso:
Substituindo os dados:
Passo 6
Agora podemos calcular o que o problema nos pede!
Determinando o trabalho específico na turbina:
Substituindo os dados:
Determinando o trabalho específico na bomba:
Calculando :
Substituindo na equação de trabalho:
E assim finalizamos a nossa questão!
Nem foi difícil né?
Até a próxima!