Um conjunto cilindro-pistão-mola linear contém de . Inicialmente a temperatura e a pressão são iguais a e . O é, então, resfriado até e nesta condição a pressão se torna igual a . Calcule a transferência de calor neste processo.

Vamos começar determinando cada volume inicial e final. Considerando o gás como ideal, temos a fórmula do gás ideal:

Olhando na tabela temos .

Convertendo as temperaturas de Celsius para Kelvin:

Aplicando para o estado inicial:

Para o estado final:

Com os volumes determinados, vamos desenhar diagrama para entendermos que tipo de área estamos lidando:

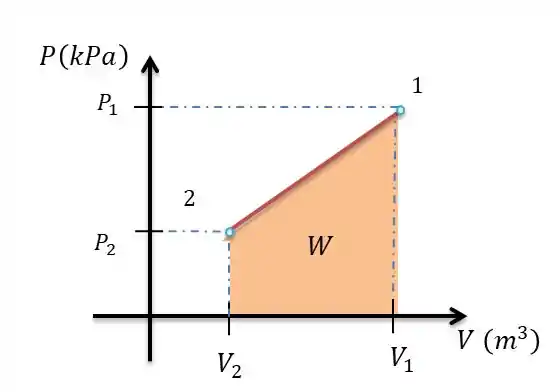
Temos que o trabalho será a área sobe a reta do diagrama.

Calculando o trabalho, temos:

Temos a área de um trapézio.

Galera antes de aplicarmos o trabalho na fórmula do calor transferido, note que, o processo que temos é de resfriamento, logo, trabalho realizado neste processo tira energia do sistema. Devido a isto, o nosso trabalho é negativo.

O nosso cálculo não abordou isso. Pois, adotamos uma abordagem gráfica e colocar ficaria incoerente com o cálculo de área.

Galera com trabalho calculado bora calcular o calor transferido.

Escrevendo a fórmula do calor, temos:

Para finalizar teremos que olhar na tabela para encontrar cada energia interna, de cada estado.

Para inicial, temos , nosso valor está entre e , fazendo uma média simples:

Para estado final, temos , como nosso valor está mais próximo de iremos fazer essa aproximação.

Todas as variáveis para o cálculo do calor transferido foram determinadas. Substituindo os cálculos na fórmula, o calor transferido é de:

É isso galera, fechou.