Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 15.Problemas - Ex. 91
Gás benzeno () a 1 atm e 77 °F é queimado durante um processo de combustão em regime permanente com 90% de ar teórico que entra na câmara de combustão a 77 °F e 1 atm. Todo o hidrogênio no combustível é queimado em , mas parte do carbono queima em CO. Calor é perdido para a vizinhança a 77 °F, e os produtos saem da câmara de combustão a 1 atm e 1.900 R. Determine:
- a transferência de calor da câmara de combustão
- destruição da exergia.
Passo 1
Existem condições operacionais estáveis.
O ar e os gases de combustão são gases ideais.
Mudanças nas energias cinética e potencial são insignificantes.
O combustível é queimado com quantidade insuficiente de ar e, portanto, os produtos conterão um pouco de CO, além de , e . A equação de combustão teórica de é:
onde é o coeficiente estequiométrico e é determinado a partir do balanço de ,
Então a equação de combustão real pode ser escrita como
O valor de é determinado a partir de um saldo de ,
Então,
Sob condições de fluxo constante, o balanço energético aplicado na câmara de combustão com se reduz a:
uma vez que todos os reagentes estão a 77 ° F.
Passo 2
Supondo que o ar e os produtos de combustão sejam gases ideais, temos.
Das tabelas:
Então,
Passo 3
Na letra b, a geração de entropia durante esse processo é determinada a partir de:
O está a 77 ° F e 1 atm e, portanto, sua entropia absoluta é
Os valores de entropia listados nas tabelas de identificação de gás são de 1 atm. Ambos o produto dos gases e o ar estão a uma pressão total de 1 atm, mas as entropias são calculadas à pressão parcial dos componentes que é onde é a fração molar do componente i. Além disso,
Os cálculos de entropia podem ser apresentados em forma de tabela como:
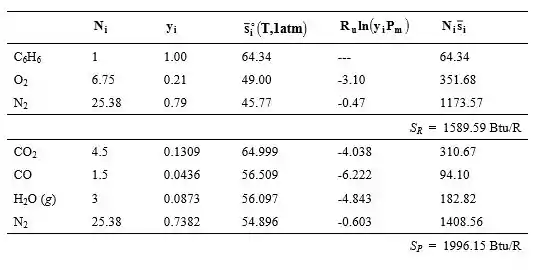
Então,
Então a exergia destruída é determinada a partir de:
(por lbmol de )
Resposta
- (por lbmol de