Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 15.Problemas - Ex. 89
O gás etileno () entra em uma câmara de combustão adiabática a 25 °C e 1 atm e é queimado com 20% de excesso de ar, que entra na câmara a 25 °C e 1 atm. A combustão é completa, e os produtos saem da câmara de combustão à pressão de 1 atm. Considerando , determine:
- a temperatura dos produtos
- a geração de entropia
- a destruição de exergia.
Passo 1
Vamos lá:
A equação de combustão, considerando 1 kmol de , é:
onde é o coeficiente estequiométrico e é determinado a partir do balanço de ,
então
sob condições de fluxo constante, a temperatura de saída dos gases do produto pode ser determinada a partir da equação da energia de fluxo constante, que reduz a:
uma vez que todos os reagentes estão no estado de referência padrão e para . Das tabelas:
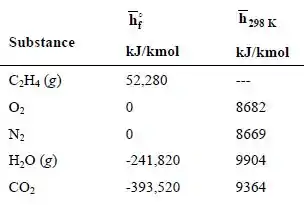
Substituindo:
Por tentativa e erro:
Passo 2
Na letra b, a geração de entropia durante esse processo adiabático é determinada a partir de
O está a 25 ° C e 1 atm e, portanto, sua entropia absoluta é 219,83 kJ / kmol · K (Tabela A-26). Os valores de entropia listados nas tabelas de gás ideais são para pressão de 1 atm. Tanto os gases do produto como a pressão total de 1 atm, mas as entropias devem ser calculadas à pressão parcial dos componentes que é igual a , onde é a fração molar do componente i. Além disso,
Os cálculos de entropia podem ser apresentados em forma de tabela como:
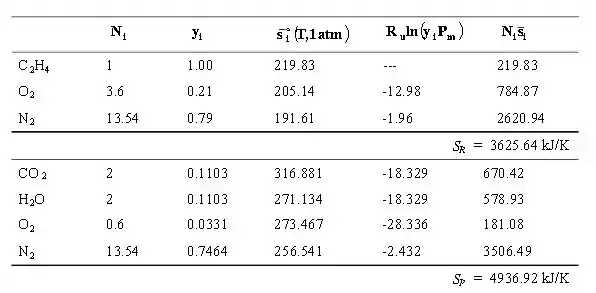
Então,
Passo 3
E na letra c: