Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 12.Problemas - Ex. 77

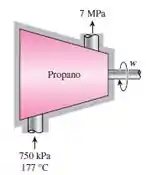
Gás propano inicialmente a 750   k P a e 177   ° C deve ser comprimido adiabaticamente e reversivelmente em um dispositivo com escoamento em regime permanente até 7000   k P a . Calcule o trabalho específico necessário para essa compressão, considerando o propano um gás ideal com calores específicos variáveis com a temperatura. Utilize os diagramas de desvio.

Passo 1

Pessoal, as propriedades do propano podem ser extraídas na tabela A - 1 , no apêndice do livro:

M = 44,097 k g k m o l ; R = 0,1885 k J k g ⋅ K ; T c r = 370   K ; P c r = 4,26   M P a

A temepratura na saída deve ser determinada pelo fato de que o processo é isentrópico e a variação da entropia molar entre a entrada e saída é zero. Quando a equação da variação da entropia é integrada com a variável de calor específico, temos:

s - 2 - s - 1 i d e a l = ∫ 1 2 c p T d T - R u ln ⁡ P 2 P 1

Quando a expressão da tablea A - 2 c é substituída no lugar de c p e é feita a integração, nós obtemos:

s - 2 - s - 1 i d e a l = ∫ 1 2 c p T d T - R u ln ⁡ P 2 P 1 = ∫ 1 2 a T + b + c T + d T 2 d T - R u ln ⁡ P 2 P 1

s - 2 - s - 1 i d e a l = a ln ⁡ T 2 T 1 + b T 2 - T 1 + c 2 T 2 2 - T 1 2 + d 3 T 2 3 - T 1 3 - R u ln ⁡ P 2 P 1

Substituindo valores, temos:

0 = - 4,04 ln ⁡ T 2 450 + 30,48 T 2 100 - 4,50 - 0,786 T 2 100 2 - 4,50 2 + 0,01058 T 2 100 3 - 4,50 3 - 8,314 ln ⁡ 7000 750

Isso nos dá,

T 2 = 532   K

Passo 2

Quando o equilíbrio de energa é aplicado ao compressor, temos:

W - e n t = h - 2 - h - 1 i d e a l = ∫ 1 2 c p d T = ∫ 1 2 a + b T + c T 2 + d T 3 d T

W - e n t = a T 2 - T 1 + b 2 T 2 2 - T 1 2 + c 3 T 2 3 - T 1 3 + d 4 T 2 4 - T 1 4

W - e n t = - 4,04 532 - 450 + 0,1524 532 2 - 450 2 - 52,4 5,32 3 - 4,50 3 + 0,7935 5,32 4 - 4,50 4

W - e n t = 9111   k J / k m o l

A potência de entrada por unidade de massa é dada por:

w e n t = W - e n t M = 9111 44,097 = 207   k J / k g

Passo 3

Os desvios de entalpia do propano nos estados especificados são determinados a partir dos diagramas generalizados (Figuras A-29):

T R 1 = T 1 T c r = 450 370 = 1 , 22

p R 1 = p 1 p c r = 0 , 5 4 , 26 = 0,17 6

Z h 1 = 0 , 136

E,

T R 2 = T 2 T c r = 532 370 = 1 , 44

p R 2 = p 2 p c r = 7 4,26 = 0 , 971

Z h 2 = 0 , 971

Portanto, podemos calcular a variação da entalpia:

h - 2 - h - 1 = w e n t = h - 2 - h - 1 i d e a l - R u T c r Z h 1 - Z h 2

w e n t = 207 - 0,1885 370 0,971 - 0,136

w e n t = 148   k J / k g

Resposta

O trabalho é igual a:

w e n t = 148   k J / k g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Complete esta tabela para H2O:
Se os dados fornecidos forem suficientes, complete as células em branco na tabela a seguir com as propriedades da água. Na última coluna, descreva a condição da água como líquido comprimido, mistura s
Considere h l v ; ela varia com a pressão? De que forma?
Mostre que a entalpia específica de um gás de Van der Waals é dada por c v T - 2 a v - R T v v - b + c o n s t a n t e .
Mostre que se F for conhecido em função de VeT . H = F - T ∂ F ∂ T V - V ∂ F ∂ V T e G = F - V ∂ F ∂ V T