Como a indução magnética dentro de um supercondutor é zero para um cilindro longo, a magnetização é igual a menos a intensidade magnética aplicada para menor que uma intensidade crítica . Para maior que , supercondutor se torna um metal normal e .

a) Esboce um gráfico da magnetização em função da intensidade aplicada. Mostre que, na transição do estado de supercondutor para o estado normal.

b) o calor de transformação é dado por

c) a diferença entre calores específicos do supercondutor e do metal normal é dada por,

Então galera para essa questão dado a magnetização menos a intensidade aplicada na intensidade crítica de , temos que na letra (a) esboçando um gráfico sobre esse termo de variações vamos ter que,

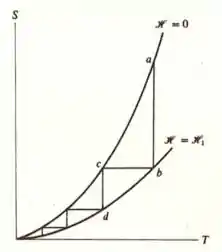
Em que a dependência da entropia passa a ser de um sistema magnético com a temperatura de

Na letra (b)determinando o valor de transformação de 1 que é representada por,

E que,

Ficando,

E por fim na letra para determinar os calores específicos dadas por,

Ficando,

Pois

Sendo a variação definida como,

Espero que eu tenha ajudado e te vejo no próximo desafio.

Até a próxima.