Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 6.Problemas - Ex. 117
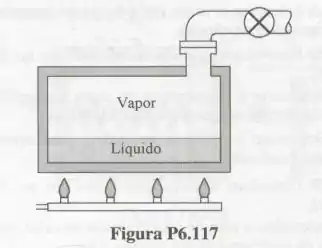
Inicialmente, o tanque de esboçado na Fig. P6.117 contém água a e título igual a . Transfere-se calor a água para a temperatura e a pressão interna aumentem. Quando a pressão na água atinge , a válvula de segurança abre e vapor saturado a passa a escoar para fora do tanque. O processo continua a até que o título se torna igual a . Nesta situação o escoamento é interrompido. Determine a massa de água que escoa para fora do tanque e o calor transferido para a água durante o processo.
Passo 1
Opa, tudo bem?
Me acompanha na resolução dessa questão?
Vem comigo!
Começamos o nosso problema aplicando a equação da continuidade no nosso processo:
Seguindo, aplicando a equação de energia:
Agora, vamos analisar os estágios do processo.
Passo 2
Estágio 1:
Pela Tabela B.1.2:
Assim:
E
Assim, conseguimos calcular :
Passo 3
Estágio 2:
Pela Tabela B.1.2:
Assim:
E
Assim, conseguimos calcular :
Passo 4
Voltando na equação da continuidade para determinarmos a massa de água que escoa para fora do tanque:
Substituindo os dados:
Para finalizarmos o nosso exercício, precisamos calcular o calor transferido para a água durante o processo, utilizando a equação de energia do Passo 1:
Com:
Pela Tabela B.1.2:
Substituindo os dados na nossa equação:
E assim terminamos nosso problema.Foi de boa né?
Te espero na próxima questão!