Enunciado

Termodinâmica - Termodinamica,Teoria Cinética e Termodinâmica Estatística, Sears e Salinger- Ed: 3º - Capítulo 8.Problemas - Ex. 9

a) Mostre que, para um líquido contendo um soluto não-volátil em equilíbrio com seu vapor a uma dada temperatura e pressão ,

Onde é a fração molar do soluto. Isto pressupõe que o soluto e o solvente se misturem como gases ideais.

b) para uma substancia pura, mostre que a pressão constante,

c) use a parte (b) para mostrar que, para uma pequena variação em à pressão constante, a parte (a) reduz-se a

d) No limite em que é pequeno,

Onde é o calor latente de vaporização. Isto mostra que a temperatura de ebulição é elevada se um soluto for adicionado a um líquido.

e) mostre como o resultado da parte de (d) pode ser usado para determinar o peso molecular de um soluto.

Passo 1

Falaaaaa rapaziada tudo blz?

Nessa questão do livro de termodinâmica de Sears e Salinger ele deseja determinar:

a) Mostre que, para um líquido contendo um soluto não-volátil em equilíbrio com seu vapor a uma dada temperatura e pressão ,

Onde é a fração molar do soluto. Isto pressupõe que o soluto e o solvente se misturem como gases ideais.

b) para uma substancia pura, mostre que a pressão constante,

c) use a parte (b) para mostrar que, para uma pequena variação em à pressão constante, a parte (a) reduz-se a

d) No limite em que é pequeno,

Onde é o calor latente de vaporização. Isto mostra que a temperatura de ebulição é elevada se um soluto for adicionado a um líquido.

e) mostre como o resultado da parte de (d) pode ser usado para determinar o peso molecular de um soluto.

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.

Passo 2

Então galerinha no primeiro desafio dessa questão ele deseja mostrar para um produto não volátil em equilíbrio com certa temperatura e pressão com sendo uma fração molar do soluto sendo,

Logo,

Na letra (b) para mostrar que a pressão é constante temos que,

Ficando,

Sendo,

Logo,

E por fim na letra para se determinar a variação,

Temos,

Ficando,

Passo 3

Na letra (d) no limite,

Onde é o calor latente, analisando o gráfico,

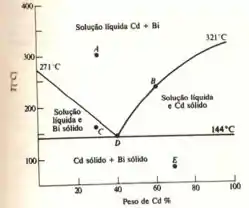
Temos,

Ficando,

E por fim na letra (e) para se determinar o peso molecular do soluto temos,

Com,

Ficando,

Espero que eu tenha ajudado e te vejo no próximo desafio.

Até a próxima.

Resposta

Exercícios de Livros Relacionados

Mostre que, se o gráfico na figura 8.5 para H = 0 corta o eixo vertical em um ponto acima do que corresponde a H = H 1 . O enunciado de inacessibilidade da terceira da terceira lei seria violado.

Mostre que, quando uma carga ∆ Z flui reversivelmente por uma célula voltaica de fem δ a temperatura e pressão constantes. a) ∆ G = δ ∆ Z ; b) ∆ H = ∆ Zd δ T d 1 T ;c) Calcule ∆ Ge∆ H para a célula, s

A equação de estado de uma película superficial pode ser escrita como σ = σ 0 1 - T T c , onde n = 1,22eσ 0 é uma constante.a) suponha que esta equação seja válida para a água e use os dados na figura

Como a indução magnética B dentro de um supercondutor é zero para um cilindro longo, a magnetização M μ 0 V é igual a menos a intensidade magnética aplicada H para H menor que uma intensidade crítica

Seja a energia radiante em um cilindro conduzida em um cicio de Carnot, semelhante ao mostrado na Figura 8.12, consistindo de uma expansão isotérmica à temperatura T , uma expansão adiabática infinite