Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Termodinamica,Teoria Cinética e Termodinâmica Estatística, Sears e Salinger- Ed: 3º - Capítulo 8.Problemas - Ex. 20

Seja a energia radiante em um cilindro conduzida em um cicio de Carnot, semelhante ao mostrado na Figura 8.12, consistindo de uma expansão isotérmica à temperatura T , uma expansão adiabática infinitesimal, em que a temperatura cai para T - d T e o retorno ao estado original efetuado por uma compressão isotérmica e uma compressão adiabática infinitesimal. Suponha P = u 3 e que U seja função somente de T .

a) Lance o ciclo em um diagrama no plano p - v ;

b) Calcule o trabalho feito pelo sistema durante o ciclo;

c) Calcule o calor que flui para o sistema durante o ciclo;

d) Mostre que U e proporcional a T ' por consideração do rendimento do ciclo.

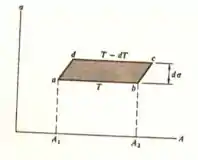
Passo 1

Falaaaaa rapaziada tudo blz?

Nessa questão do livro de termodinâmica de Sears e Salinger Seja a energia radiante em um cilindro conduzida em um cicio de Carnot, semelhante ao mostrado na Figura 8.12, consistindo de uma expansão isotérmica à temperatura T , uma expansão adiabática infinitesimal, em que a temperatura cai para T - d T e o retorno ao estado original efetuado por uma compressão isotérmica e uma compressão adiabática infinitesimal. Suponha P = u 3 e que U seja função somente de T .

a) Lance o ciclo em um diagrama no plano p - v ;

b) Calcule o trabalho feito pelo sistema durante o ciclo;

c) Calcule o calor que flui para o sistema durante o ciclo;

d) Mostre que U e proporcional a T ' por consideração do rendimento do ciclo.

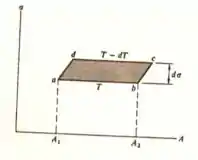
Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.

Passo 2

Então galerinha determinando o lance do ciclo na letra (a) no diagrama para p - v , temos sua representação por,

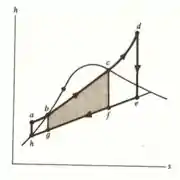
Já na letra (b) para determinar o trabalho feito pelo sistema, temos

∂ U ∂ T = V 2 - V 1 3

Ficando,

∂ ' U = 3 V 2 - V 1 2

Na letra ( c ) para calcular o calor no sistema durante o ciclo temos,

U = 1 3 u v 4

Ficando a derivada como,

∂ U = 4 3 μ V 2 - V 1 3

E por fim na letra (d) para mostrar que μ é proporcional a T no rendimento do ciclo temos,

C t = ∂ T ∂ H H

Ficando,

C T ' = T ∂ T ∂ H

Espero que eu tenha ajudado e te vejo no próximo desafio.

Até a próxima.

Resposta

a) gráfico no passo anterior

b) ∂ ' U = 3 V 2 - V 1 2

c) ∂ U = 4 3 μ V 2 - V 1 3

d) C T ' = T ∂ T ∂ H

Exercícios de Livros Relacionados

Dióxido de carbono a 15M P a é injetado no topo de um poço com 5k m de profundidade. Esta operação faz parte de um processo de recuperação de petróleo não extraído. Sabendo que a temperatura do fluido
Desenvolva a expressão para a pressão na superfície inferir de um poço d’água profundo em função da compressibilidade isotérmica, β T . Utilize hipóteses iguais aquelas empregadas na obtenção da equaç
Um volume V é dividido em duas partes por uma separação diatérmica sem atrito. Há n A moles de um gás ideal A de um lado da separação, e n B moles de um gás Ideal B , do outro lado. a) Calcule a varia
Um diagrama fase é um diagrama temperatura-composição para um sistema de dois componentes em várias fases. Um diagrama de fases Idealizado para o sistema cadmio bismuto é mostrado na Figura 8.11 para
Uma turbina a vapor opera em um ciclo de Rankine reversível. Vapor superaquecido entre na turbina a uma pressão de 100l bp o l - 2 e uma temperatura de 800 ° F . A pressão do vapor na exaustão é de 15