Um motor moderno de 1,8 L, de quatro cilindros e alta rotação, e com ignição por compressão de quatro tempos, funciona no ciclo dual ideal com uma razão de compressão de 16. O ar está a 95 kPa e 70 °C no início do processo de compressão, e a velocidade do motor é de 2.200 rpm. Quantidades iguais de combustível são queimadas a um volume e a uma pressão constantes. A pressão máxima permitida no ciclo é de 7,5 MPa devido às limitações de resistência do material. Usando calores específicos constantes a 1.000 K, determine:
- a temperatura máxima no ciclo
- o trabalho líquido produzido e a eficiência térmica
- a pressão média efetiva
- a potência líquida.
- a eficiência de segunda lei do ciclo e a taxa com que a exergia é eliminada com os gases de exaustão.
Determine também
Passo 1
Vamos assumir que:
As premissas do padrão aéreo são aplicáveis.
As alterações cinéticas e potenciais de energia são insignificantes.
O ar é um gás ideal com aquecimentos específicos constantes.
Sabemos que as propriedades do ar a 1000 K são:
Vamos utilizar esse gráfico abaixo para a resolução dos tópicos:
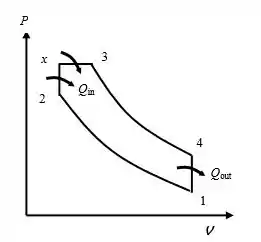
Passo 2
Agora vamos para a letra a)
O volume livre e o volume total do motor no início do processo de compressão (estado 1) são:
Processo 1- compressão isentrópica
Processo 2-x e x-3: processos de adição de calor de volume constante e pressão constante:
Passo 3
Agora, na letra b, temos:
Processo 3-4: expansão isentrópica.
Processo 4-1: rejeição de calor em volume constante.
A produção líquida de trabalho e a eficiência térmica são:
Passo 4
Na letra c, a pressão efetiva média é determinada como sendo:
Passo 5
Na letra d, a potência da rotação do motor de 3500 rpm é:
Observe que existem duas rotações em um ciclo em motores a quatro tempos.
Passo 6
E por fim, na letra e, temos que a eficácia da segunda lei do ciclo é definida como a razão entre a eficiência térmica real e a máxima eficiência térmica possível (eficiência de Carnot). Consideramos a temperatura e a pressão do estado morto em 25ºC e 100 kPa.
e
A taxa de exergia dos gases de escape é determinada da seguinte forma: