Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 10.Problemas - Ex. 79
O motor térmico indicado na é alimentado com ar nas condições do ambiente . A taxa de transferência de calor do reservatório térmico que apresenta temperatura igual a para o motor é igual a por quilograma de ar que escoa no equipamento e, numa certa região da máquina, ocorre uma transferência de calor da máquina para um reservatório térmico que apresenta temperatura igual a . A pressão e a temperatura do ar na seção de descarga do motor são iguais a . Determine as eficiências baseadas na primeira e na segunda lei da termodinâmica deste motor.
Passo 1
Oi. Precisa de ajuda nessa questão? Vem comigo!
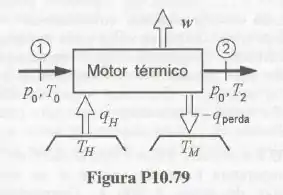
Neste exercício nós temos uma valiosa ferramenta pra resolução, que é a figura. Em exercícios de termodinâmica nós precisamos imaginar a situação que está acontecendo no nosso espaço analisado e a figura desta questão já nos deu todo o processo.
Vamos então identificar cada elemento da figura relacionando com os dados do enunciado. Temos que:
Passo 2
Agora que identificamos cada elemento, vamos ao que o exercício quer. Temos que determinar as eficiências deste motor baseadas na primeira e na segunda lei.
A eficiência baseada na primeira lei é dada por:
Onde é o trabalho líquido gerado e o calor fornecido à máquina.
A eficiência baseada na segunda lei é dada por:
Onde é o trabalho reversível da máquina.
Nas duas fórmulas vamos precisar do trabalho de eixo , então vamos em busca dele. Aplicando a equação da energia para o motor, temos que:
Portanto:
Passo 3
Precisamos encontrar os valores de entalpia dos estados de entrada e saída . Analisando as tabelas de propriedades termodinâmicas, temos que:
Podemos encontrar também as entropias padrões dos dois estados pois precisaremos depois.
Aplicando os valores na equação do trabalho, temos que:
A eficiência baseada na primeira lei será:
Ou:
Passo 4
Para descobrir a eficiência baseada na segunda lei, precisamos do trabalho reversível. Ele é dado por:
Onde é a irreversibilidade do processo. Para este sistema, temos que:
Temos que:
Como a pressão do processo é constante, temos que:
Passo 5
Portanto, o trabalho reversível será:
A eficiência baseada na segunda lei será:
Ou:
Pronto, resolvida. Vamos pra próxima?