Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 5.Problemas - Ex. 33

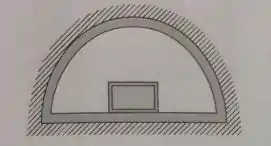
Um reator com volume de 1   m 3 , cheio d’água, está a 20   M P a e 360 ° C dentro de um vaso de contenção conforme mostrado na Fig. P5.33. O vaso é bem isolado e, inicialmente, está evacuado, devido a uma falha, o reator rompe-se e a água preenche o ambiente de contenção. Determine o volume mínimo do vaso para que a pressão final nele não exceda 200   k P a .

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Nós temos os seguintes dados:

V 1 = 1   m 3

T = 360 ° C

P 1 = 20   M P a

P 2 = 200   k P a

Da tabela B.1.2, correspondente a P = 20   M P a , nós podemos encontrar a temperatura de saturação

T s a t = 365,81 ° C

Nós podemos ver que T s a t > T , então a água está no estado de líquido comprimido. Da tabela de água comprimida (tabela B.1.4), com a temperatura T = 360 ° C , nós podemos obter o volume específico e a energia interna

v 1 = 0,001823 m 3 k g

u 1 = 1702,78 k J k g

A sala é isolada e evacuada, para que não haja alteração na energia interna:

u 2 = u 1 = 1702,78 k J k g

A massa da água é igual a

m = V 1 v 1 = 1 0,001823 = 548,54   k g

Passo 2

Da tabela B.1.2, com pressão P = 200   k P a , nós podemos obter os seguintes resultados:

v f = 0,001061 m 3 k g

v f g = 0,88467 m 3 k g

u f = 504,47 k J k g

u f g = 2025,02 k J k g

A energia interna específica final é dada por:

u 2 = u f + x ∙ u f g

Podemos calcular o fator de qualidade

x = u 2 - u f u f g = 1702,78 - 504,47 2025,02 = 0,592

Podemos calcular agora o volume específico final:

v 2 = v f + x ∙ v f g = 0,001601 + 0,592 ∙ 0,88467 = 0,525 m 3 k g

O volume mínimo da sala para que a pressão final não exceda P = 200   k P a é igual a

V = m ∙ v 2 = 548,54 ∙ 0,52457 = 288   m 3

Resposta

V = 288   m 3

Exercícios de Livros Relacionados

Uma massa de 12 kg de vapor saturado de refrigerante-134a está contida em arranjo pistão-cilindro a 240 kPa. Uma quantidade de 300 kJ de calor é então transferida para o refrigerante a uma pressão con
Um vaso rígido bem isolado contém 3 kg de água líquida saturada a 40 °C. O vaso também contém uma resistência elétrica que consome 10 ampères quando 50 volts são aplicados. Determine a temperatura fin
Vapor de água saturado a 200 °C é condensado até se tornar líquido saturado a 50 °C em um arranjo pistão-cilindro com mola. Determine a transferência de calor para esse processo, em kJ/kg.
Uma sala bem isolada de 4 m × 4 m × 5 m, inicialmente a 10 °C, é aquecida pelo radiador de um sistema de aquecimento a vapor. O radiador tem um volume de 15 L e contém vapor superaquecido a 200 kPa e
Usando as equações do Prob. 4-151, determine a energia explosiva de 20 m³ de vapor a 10 Mpa e 500 °C, considerando que o vapor se condensa e se torna líquido a 25 °C depois da explosão. A quantos quil