Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 4.Problemas - Ex. 143
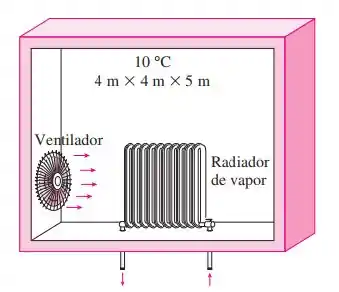
Uma sala bem isolada de 4 m 4 m 5 m, inicialmente a 10 °C, é aquecida pelo radiador de um sistema de aquecimento a vapor. O radiador tem um volume de 15 L e contém vapor superaquecido a 200 kPa e 200 °C. Sob essas condições, as válvulas de entrada e saída do radiador são fechadas. Um ventilador de 120 W é usado para circular o ar na sala. Observa-se que a pressão do vapor cai a 100 kPa depois de 30 minutos, como resultado da transferência de calor para a sala. Considerando os calores específicos do ar constantes, determine a temperatura média do ar após os 30 minutos. Considere que a pressão do ar permanece constante a 100 kPa.
Passo 1
Bom, nessa questão primeiro você precisa definir qual sistema vai ser analisado de forma inicial, que nesse caso vamos escolher o radiador. A equação de balanço de energia para o radiador vai ser:
Nessa equação, como o calor está sendo transferido do sistema para o ambiente, ele vem acompanhado do sinal negativo. A partir disso, determinamos as propriedades do estado inicial e final utilizando as tabelas de água (Tabela A-4, A-5 e A-6)
Em 2, temos mistura líquido-vapor, logo:
Assim, o título é:
E a energia interna em 2 é:
A massa de água no radiador é:
Com todas essas informações, podemos substituir os valores na equação de balanço de energia no radiador, e com isso, o calor transferido do radiador é:
Passo 2
Agora vamos estabelecer que nosso sistema é a sala. A equação de balanço de energia para esse sistema é:
O trabalho de fronteira aqui existe para equilibrar com o trabalho do ventilador de forma a manter a pressão constante. Como , temos que:
A massa de ar contida na sala, que tem um volume de ar , é calculada por:
Outra informação importante é o trabalho realizado pelo ventilador, calculado por:
Passo 3
O calor específico na temperatura da sala, de acordo com a Tabela A-2, é kJ/kg.K. Assim, substituindo os valores na equação de balanço de energia para a sala: