Um recipiente rígido preenchido com um gás ideal é aquecido enquanto o gás é liberado, e de tal modo que a temperatura do gás remanescente no recipiente permanece constante. Esse recipiente tem uma única saída. Obtenha uma expressão para o fluxo de massa na saída como uma função da taxa de variação da pressão no recipiente.
Passo 1
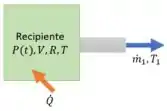
O recipiente é o nosso volume de controle. Como a massa dele está sendo modificada, vamos aplicar um balanço de massas:
Não há massa entrando no sistema, e a massa que sai é
Passo 2
Vamos aplicar a lei dos gases em um instante qualquer do volume de controle, onde a pressão e o volume do volume de controle serão iguais ao produto da massa, da temperatura e da constante do gás do volume de controle.
Isolamos a massa:
Como um gás sempre ocupa todo o volume disponível, o volume não varia. A questão também afirma que a temperatura não varia. Então, à medida que a massa escapa do recipiente, a pressão diminui.
Derivando a massa em relação ao tempo:
Passo 3
Vamos igualar as duas expressões:
Então, a vazão de massa é: