Reconsidere o Prob. 10-104. Usando o EES (ou outro programa), determine a pressão de extração ótima para o aquecedor de água de alimentação aberto que maximiza a eficiência térmica do ciclo.
Passo 1
Tá legal, o que precisamos fazer é fornecer os dados do enunciado do Prob. 10-104 para o EES para que ele determine o valor das propriedades nos pontos de interesse, e após isso, devemos escrever exatamente as mesmas equações que usamos para resolver o Prob. 10-104, só que deixando em função da pressão de extração para o aquecedor de água de alimentação aberto.
Passo 2
Então, o código em EES que resolve o nosso problema é dado a seguir:
"Dados fornecidos no problema 10-104"
P_caldeira=6000 [kPa]
P_aaaf1=3000 [kPa]
P_aaaf2=1800 [kPa]
P_reaq=800 [kPa]
"P_aaaa=100 [kPa]"
P_condensador=7.5 [kPa]
T_turbina=500 [C]
Fluid$='STEAM'
"Entalpias e entropias das turbinas"
h[13]=enthalpy(Fluid$; P=P_caldeira; T=T_turbina)
s[13]=entropy(Fluid$; P=P_caldeira; T=T_turbina)
h[14]=enthalpy(Fluid$; P=P_aaaf1; s=s[13])
h[15]=enthalpy(Fluid$; P=P_aaaf2; s=s[13])
h[16]=enthalpy(Fluid$; P=P_reaq; s=s[13])
h[17]=enthalpy(Fluid$; P=P_reaq; T=T_turbina)
s[17]=entropy(Fluid$; P=P_reaq; T=T_turbina)
h[18]=enthalpy(Fluid$; P=P_aaaa, s=s[17])
h[19]=enthalpy(Fluid$; P=P_condensador; s=s[17])
"Análise da bomba 1"
h[1]=enthalpy(Fluid$; P=P_condensador; x=0)
v[1]=volume(Fluid$; P=P_condensador; x=0)
w_b1=v[1]*(P_aaaa-P_condensador)
h[2]=h[1]+w_b1
"Análise da bomba 2"
h[3]=enthalpy(Fluid$; P=P_aaaa; x=0)
v[3]=volume(Fluid$; P=P_aaaa; x=0)
w_b2=v[3]*(P_aaaf2-P_aaaa)
h[4]=h[3]+w_b2
"Análise da bomba 3"
h[5]=enthalpy(Fluid$; P=P_aaaf2; x=0)
T[5]=temperature(Fluid$; P=P_aaaf2; x=0)
v[5]=volume(Fluid$; P=P_aaaf2; x=0)
w_b3=v[5]*(P_aaaf1-P_aaaf2)
h[6]=h[5]+w_b3
"Análise da bomba 4"
h[9]=enthalpy(Fluid$; P=P_aaaf1; x=0)
T[9]=temperature(Fluid$; P=P_aaaf1; x=0)
v[9]=volume(Fluid$; P=P_aaaf1; x=0)
w_b4=v[5]*(P_caldeira-P_aaaf1)
h[10]=h[9]+w_b4
"Balanços de massa nas turbinas"
x+y+z=1
m+n=z
"Análise do balanço de massa no aquecedor aberto "
m*h[18]+n*h[2]=z*h[3]
"Análise do balanço de massa no aquecedor fechado 2"
T[7]=T[5]
h[7]=enthalpy(Fluid$; P=P_aaaf1; T=T[7])
z*h[4]+y*h[15]=z*h[7]+y*h[5]
"Análise do balanço de massa no aquecedor fechado 1"
T[11]=T[9]
h[11]=enthalpy(Fluid$; P=P_condensador; T=T[11])
(y+z)*h[8]+x*h[14]=(y+z)*h[11]+x*h[9]
"Análise na saída do aquecedor fechado 2"
z*h[7]+y*h[6]=(y+z)*h[8]
"Análise na saída do aquecedor fechado 1"
x*h[10]+(y+z)*h[11]=1*h[12]
"Análise do ciclo"
w_T_AP=x*(h[13]-h[14])+y*(h[13]-h[15])+z*(h[13]-h[16])
w_T_BP=m*(h[17]-h[18])+n*(h[17]-h[19])
q_e=h[13]-h[12]+z*(h[17]-h[16])
q_s=n*(h[19]-h[1])
Eta=1-q_s/q_e
Passo 3
Então, com esse código, obtemos a seguinte tabela paramétrica com a pressão de extração do aquecedor de água de alimentação aberto e a eficiência do sistema:
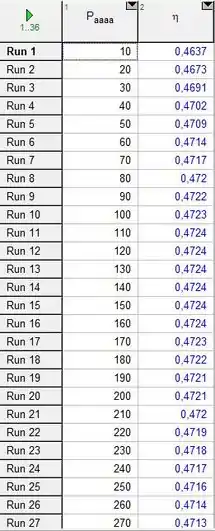
E o seguinte gráfico ilustrando os dados obtidos:

Então, observando o gráfico e os dados obtidos na tabela paramétrica, a eficiência ótima seria:
E estaria dentro do intervalo de pressões: