Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 10.Problemas - Ex. 40
Uma usina de potência a vapor opera em um ciclo de Rankine ideal com reaquecimento entre os limites de pressão de 15 MPa e 10 kPa. O fluxo de massa de vapor de água no ciclo é de 12 kg/s. O vapor entra em ambos os estágios da turbina a 500 °C. Considerando que o conteúdo de umidade do vapor na saída da turbina de baixa pressão não deve exceder 10%, determine (a) a pressão na qual ocorre o reaquecimento, (b) a taxa total de consumo de calor na caldeira e (c) a eficiência térmica do ciclo. Mostre também o ciclo em um diagrama T-s que inclua as linhas de saturação.
Passo 1
Oi pessoal, tudo bem?
Consideremos o esboço para este problema:
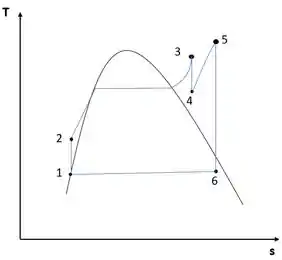
Bem, para início de análise, o problema indica que o estado 1 encontra-se em líquido saturado. Sabemos que o estado 1 encontra-se à mesma pressão do estado 6. Então, utilizando o auxílio das tabelas A.4, A.5 e A6, é possível encontrar algumas relações termodinâmicas.
Passo 2
Temos a pressão de , na tabela de líquido saturado, podemos obter:
Sabendo que o trabalho específico pode ser dado por :
Passo 3
O estado 3 está em vapor superaquecido com e temperatura Então:
Mas sabemos que e o título é , portanto, das tabelas:
Do estado 4, só sabemos que possui mesma pressão do estado 5 e entropia do estado 3. O estado 5 está em vapor superaquecido com porém não sabemos ainda a sua pressão ou entropia.
Mas sabemos que e o título é , portanto, das tabelas:
Para encontrar o :
Agora, sabendo a temperatura e a entropia no estado 5 (), podemos encontrar nas tabelas: .
E então, como :
Passo 4
Então, a taxa de calor que entra é:
A taxa de rejeição de calor é:
Assim, a eficiência térmica é:
Resposta
Portanto: