Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 132

Reelabore o P r o b .   9 – 131 E , considerando que cada compressor tenha uma eficiência isentrópica de 85 % e que cada turbina tem uma eficiência isentrópica de 90 % .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O ciclo Brayton real com dois estágios de compressão e dois estágios de expansão com regeneração é dado pelo seguinte diagrama T - s :

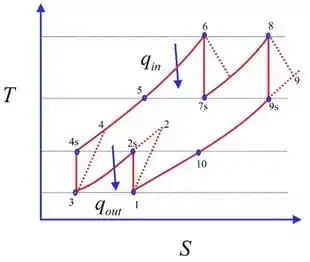
Como devemos considerar calores específicos constantes à temperatura ambiente, do processo 1 → 2 s , temos que:

T 2 s T 1 = P 2 P 1 k - 1 k

Temos que:

T 2 s = T 1 ⋅ P 2 P 1 k - 1 k

Logo:

T 2 s = T 1 ⋅ r p k - 1 k

Nos foi dada a razão de pressão total, portanto a razão de pressão em cada equipo é de:

r p = 12

r p = 3,46

Substituindo os valores temos que:

T 2 s = 460 + 60 ⋅ 3,46 1,4 - 1 1,4

T 2 s = T 4 s = 741 , 6   R

As temperaturas reais serão:

T 2 = T 4 = 520 + 741 - 520 0,85

T 2 = T 4 = 780,7   R

Passo 2

Como a temperatura do ar frio é aumentada em 50   ° F no regenerador, temos que:

T 5 = T 7 = T 9 = T 4 + 50

T 5 = T 7 = T 9 = 780 , 7 + 50

T 5 = T 7 = T 9 = 830,7   R

Para a expansão 6 s → 7 , temos que:

T 7 T 6 s = P 7 P 6 k - 1 k

Como:

P 7 P 6 = 1 r p

Substituindo os valores, temos que:

T 6 s = T 7 r p k - 1 k

T 6 s = 830,7 3,46 1,4 - 1 1,4

T 6 s = T 8 s = 11 85   R

As temperaturas reais serão:

T 6 = T 8 = 830,7 + 0,9 ( 1185 - 830,7 )

T 6 = T 8 = 1150   R

Passo 3

O calor fornecido será:

q e n t = 2 c p T 6 - T 5

q e n t = 2 ⋅ 0,24 ⋅ 1150 - 830,7

q e n t = 153,3   B t u / l b m

O fluxo de massa será:

m ˙ = Q ˙ e n t q e n t

m ˙ = 500 153,3

m ˙ = 3 , 262   l b m / s

Passo 4

Aplicando a primeira lei para a expansão 6 → 7 , temos que:

W ˙ 6 → 7 s a i = m ˙ c p T 6 - T 7

Substituindo os valores, temos que:

W ˙ 6 → 7 s a i = 3,262 ⋅ 0,24 ⋅ 11 50 - 830,7 ⋅ 1 k W 0,94782   B t u / s

W ˙ 6 → 7 s a i = 263 , 7   k W

A mesma quantidade de potência é produzida durante o processo 8 → 9 , logo:

W ˙ 6 → 7 s a i = W ˙ 8 → 9 s a i = 263 , 7   k W

Aplicando a primeira lei para a compressão 1 → 2 , temos que:

W ˙ 1 → 2 e n t = m ˙ c p T 2 - T 1

Substituindo os valores, temos que:

W ˙ 1 → 2 e n t = 3,262 ⋅ 0,24 ⋅ 780,7 - 520 ⋅ 1 k W 0,94782   B t u / s

W ˙ 1 → 2 e n t = 215,3   k W

A mesma quantidade de potência é produzida durante o processo 3 → 4 , logo:

W ˙ 1 → 2 e n t = W ˙ 3 → 4 e n t = 215,3   k W

A taxa de calor rejeitado pelo ciclo será:

Q ˙ s a i = 2 m ˙ c p T 2 - T 3

Q ˙ s a i = 2 ⋅ 3,262 ⋅ 0,24 ⋅ 780,7 - 520

Q ˙ s a i = 408,2   B t u / s

Resposta

W ˙ 6 → 7 s a i = W ˙ 8 → 9 s a i = 263,7   k W

W ˙ 1 → 2 e n t = W ˙ 3 → 4 e n t = 215,3   k W

Q ˙ s a i = 408,2   B t u / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os processos utilizados no ciclo Brayton são iguais àqueles do ciclo Rankine. Porque os diagramas T - s e p - v desses ciclos parecem tão diferentes?
É sempre possível adicionar um regenerador num ciclo Brayton? O que ocorre se a relação de compressão for aumentada?
A potência gerada num ciclo de Brayton é 14M W . A relação de compressão utilizada no ciclo é 16 : 1 e o ar entra no compressor a 17° C e 100k P a . Sabendo que o processo de combustão no ciclo pode s
Um regenerador ideal é incorporado ao ciclo padrão a ar Brayton ideal descrito no Prob. 11.68. Calcule o rendimento térmico do ciclo que apresenta esta modificação
Considere uma instalação estacionária de turbina a gás que opera segundo o ciclo Brayton ideal e que fornece uma potência de 100M W a um gerador elétrico. A temperatura mínima do ciclo é 300K e a máxi