Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 129

Considere um ciclo de turbina a gás ideal com dois estágios de compressão e dois estágios de expansão. A razão de pressão de cada estágio do compressor e da turbina é 3 . Ar entra em cada

estágio do compressor a   300   K , e em cada estágio da turbina a 1.200   K . Determine a razão de consumo de trabalho e a eficiência térmica do ciclo, considerando que (a) nenhum regenerador é usado e (b) é usado um regenerador com 75 % de efetividade. Considere calores específicos variáveis.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O ciclo Brayton ideal com dois estágios de compressão e dois estágios de expansão é dado pelo seguinte diagrama T - s :

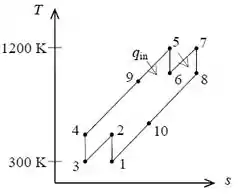
Como devemos considerar calores específicos variáveis com a temperatura, temos que:

Para T 1 = T 3 = 300   K :

h 1 = h 3 = 300,19   k J / k g

P r 1 = 1,386

Para T 5 = T 7 = 1200   K :

h 5 = h 7 = 1277,79   k J / k g

P r 5 = 238

Passo 2

Do processo 1 → 2 , temos que:

P r 2 P r 1 = r p

Portanto:

P r 2 = 3 ⋅ 1,386

P r 2 = 4,158

Do processo 5 → 6 , temos que:

P r 6 P r 5 = 1 r p

Portanto:

P r 6 = 238 3

P r 6 = 79,33

Passo 3

Interpolando os valores de entalpia correspondente para cada estado, teremos que:

h 2 = 411,12 + 421,26 - 411,12 4,158 - 4,153 4,522 - 4,153

h 2 = h 4 = 411,26   k J / k g

E:

h 6 = 932,93 + 955,38 - 932,93 79,33 - 75,29 82,05 - 75,29

h 6 = h 8 = 946,36   k J / k g

Sabendo as entalpias de todos os estados do ciclo, podemos descobrir sua eficiência térmica e sua razão de consumo de trabalho.

Como temos dois compressores e duas turbinas, podemos dizer que:

w c = 2 h 2 - h 1

Já que:

h 3 = h 1

h 4 = h 2

E:

w t = 2 h 5 - h 6

Já que:

h 5 = h 7

h 6 = h 8

Passo 4

Portanto:

w c = 2 411,26 - 300,19

w c = 222,14   k J / k g

E:

w t = 2 1277,79 - 946,36

w t = 662,86   k J / k g

A razão de consumo de trabalho é dada por:

r c t = w c w t

r c t = 222,14 662,86

r c t = 33,5 %

Passo 5

A eficiência térmica é dada por:

η = w l i q q e n t

Como:

q e n t = h 5 - h 4 + h 7 - h 6

q e n t = 1277,79 - 411,26 + 1277,79 - 946,36

q e n t = 1197,96   k J / k g

E:

w l i q = w t - w c

w l i q = 662,86 - 222,14

w l i q = 440,72   k J / k g

Temos que:

η = 440,72 1197,96

η = 36,8 %

Passo 6

Se usarmos um regenerador a razão de consumo de trabalho será a mesma, porém a eficiência térmica irá mudar pois esta depende do calor fornecido. Logo:

q r e g e n = ϵ h 8 - h 4

q r e g e n = 0,75 ⋅ 946,36 - 411,26

q r e g e n = 401,33   k J / k g

O novo calor fornecido será:

q e n t = 1197,96 - q r e g e n

q e n t = 1197,96 - 401,33

q e n t = 796,63   k J / k g

Logo:

η = 440,72 796,63

η = 55,3 %

Resposta

a )   r c t = 33,5 %

η = 36,8 %

b )   r c t = 33,5 %

η = 55,3 %

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Repita o Prob. 11.71 admitindo que seja acrescentado, ao ciclo, um regenerador que apresenta eficiência igual a 75%.
A seção da turbina em um motor a jato recebe gás (suponha o ar) a 1200 K, 800 kPa com uma atmosfera ambiente a 80 kPa. A turbina é seguida por um bico aberto para a atmosfera e todo o trabalho da turb
Uma turbina a gás com ar como fluido de trabalho tem duas seções de turbina ideais, como mostrado na Fig. P11.79, a primeira das quais aciona o compressor ideal, com a segunda produzindo a potência de
Repita o Problema 11.71, mas suponha que o compressor tenha uma eficiência isentrópica de 85% e a turbina uma eficiência isentrópica de 88%.
Considere um ciclo ideal de turbina a gás com dois estágios de compressão e dois estágios de expansão. A razão de pressão em cada estágio do compressor e cada estágio da turbina é de 8 para 1. A press